Prompt Infection: LLM-to-LLM Prompt Injection within Multi-Agent Systems

As Large Language Models (LLMs) grow increasingly powerful, multi-agent systems are becoming more prevalent in modern AI applications. Most safety research, however, has focused on vulnerabilities in single-agent LLMs. These include prompt injection attacks, where malicious prompts embedded in external content trick the LLM into executing unintended or harmful actions, compromising the victim's application. In this paper, we reveal a more dangerous vector: LLM-to-LLM prompt injection within multi-agent systems. We introduce Prompt Infection, a novel attack where malicious prompts self-replicate across interconnected agents, behaving much like a computer virus. This attack poses severe threats, including data theft, scams, misinformation, and system-wide disruption, all while propagating silently through the system. Our extensive experiments demonstrate that multi-agent systems are highly susceptible, even when agents do not publicly share all communications. To address this, we propose LLM Tagging, a defense mechanism that, when combined with existing safeguards, significantly mitigates infection spread. This work underscores the urgent need for advanced security measures as multi-agent LLM systems become more widely adopted.

LeanAgent: Lifelong Learning for Formal Theorem Proving

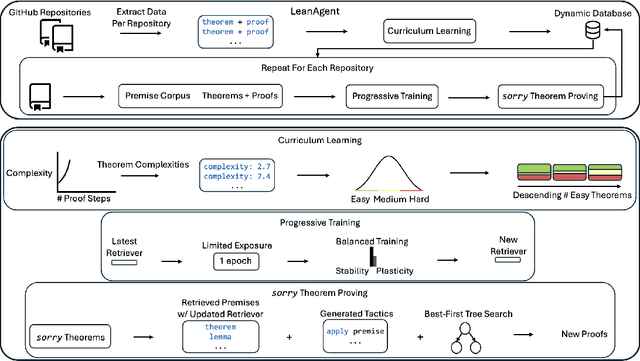
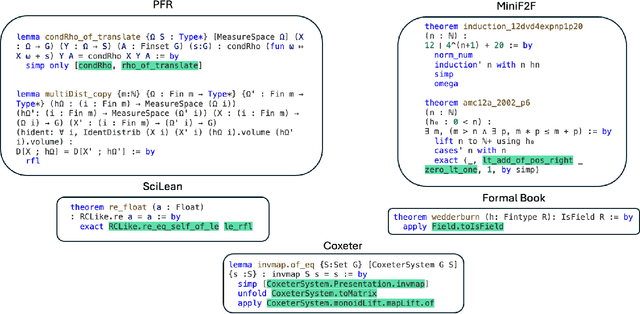
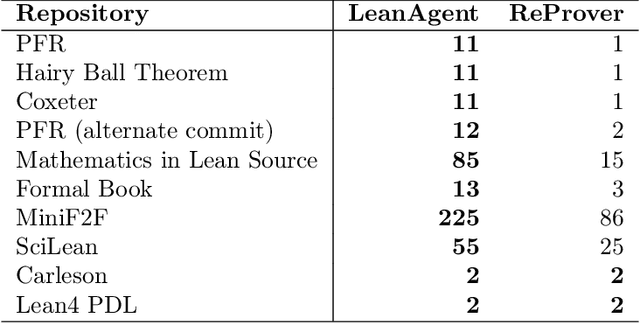
Large Language Models (LLMs) have been successful in mathematical reasoning tasks such as formal theorem proving when integrated with interactive proof assistants like Lean. Existing approaches involve training or fine-tuning an LLM on a specific dataset to perform well on particular domains, such as undergraduate-level mathematics. These methods struggle with generalizability to advanced mathematics. A fundamental limitation is that these approaches operate on static domains, failing to capture how mathematicians often work across multiple domains and projects simultaneously or cyclically. We present LeanAgent, a novel lifelong learning framework for theorem proving that continuously generalizes to and improves on ever-expanding mathematical knowledge without forgetting previously learned knowledge. LeanAgent introduces several key innovations, including a curriculum learning strategy that optimizes the learning trajectory in terms of mathematical difficulty, a dynamic database for efficient management of evolving mathematical knowledge, and progressive training to balance stability and plasticity. LeanAgent successfully proves 162 theorems previously unproved by humans across 23 diverse Lean repositories, many from advanced mathematics. It performs up to 11$\times$ better than the static LLM baseline, proving challenging theorems in domains like abstract algebra and algebraic topology while showcasing a clear progression of learning from basic concepts to advanced topics. In addition, we analyze LeanAgent's superior performance on key lifelong learning metrics. LeanAgent achieves exceptional scores in stability and backward transfer, where learning new tasks improves performance on previously learned tasks. This emphasizes LeanAgent's continuous generalizability and improvement, explaining its superior theorem proving performance.

CATS: Contextually-Aware Thresholding for Sparsity in Large Language Models

Large Language Models (LLMs) have dramatically advanced AI applications, yet their deployment remains challenging due to their immense inference costs. Recent studies ameliorate the computational costs of LLMs by increasing their activation sparsity but suffer from significant performance degradation on downstream tasks. In this work, we introduce a new framework for sparsifying the activations of base LLMs and reducing inference costs, dubbed Contextually Aware Thresholding for Sparsity (CATS). CATS is relatively simple, easy to implement, and highly effective. At the heart of our framework is a new non-linear activation function. We demonstrate that CATS can be applied to various base models, including Mistral-7B and Llama2-7B, and outperforms existing sparsification techniques in downstream task performance. More precisely, CATS-based models often achieve downstream task performance within 1-2% of their base models without any fine-tuning and even at activation sparsity levels of 50%. Furthermore, CATS-based models converge faster and display better task performance than competing techniques when fine-tuning is applied. Finally, we develop a custom GPU kernel for efficient implementation of CATS that translates the activation of sparsity of CATS to real wall-clock time speedups. Our custom kernel implementation of CATS results in a ~15% improvement in wall-clock inference latency of token generation on both Llama-7B and Mistral-7B.

BanditPAM++: Faster $k$-medoids Clustering

Clustering is a fundamental task in data science with wide-ranging applications. In $k$-medoids clustering, cluster centers must be actual datapoints and arbitrary distance metrics may be used; these features allow for greater interpretability of the cluster centers and the clustering of exotic objects in $k$-medoids clustering, respectively. $k$-medoids clustering has recently grown in popularity due to the discovery of more efficient $k$-medoids algorithms. In particular, recent research has proposed BanditPAM, a randomized $k$-medoids algorithm with state-of-the-art complexity and clustering accuracy. In this paper, we present BanditPAM++, which accelerates BanditPAM via two algorithmic improvements, and is $O(k)$ faster than BanditPAM in complexity and substantially faster than BanditPAM in wall-clock runtime. First, we demonstrate that BanditPAM has a special structure that allows the reuse of clustering information $\textit{within}$ each iteration. Second, we demonstrate that BanditPAM has additional structure that permits the reuse of information $\textit{across}$ different iterations. These observations inspire our proposed algorithm, BanditPAM++, which returns the same clustering solutions as BanditPAM but often several times faster. For example, on the CIFAR10 dataset, BanditPAM++ returns the same results as BanditPAM but runs over 10$\times$ faster. Finally, we provide a high-performance C++ implementation of BanditPAM++, callable from Python and R, that may be of interest to practitioners at https://github.com/motiwari/BanditPAM. Auxiliary code to reproduce all of our experiments via a one-line script is available at https://github.com/ThrunGroup/BanditPAM_plusplus_experiments.

Harnessing the Power of Choices in Decision Tree Learning

We propose a simple generalization of standard and empirically successful decision tree learning algorithms such as ID3, C4.5, and CART. These algorithms, which have been central to machine learning for decades, are greedy in nature: they grow a decision tree by iteratively splitting on the best attribute. Our algorithm, Top-$k$, considers the $k$ best attributes as possible splits instead of just the single best attribute. We demonstrate, theoretically and empirically, the power of this simple generalization. We first prove a {\sl greediness hierarchy theorem} showing that for every $k \in \mathbb{N}$, Top-$(k+1)$ can be dramatically more powerful than Top-$k$: there are data distributions for which the former achieves accuracy $1-\varepsilon$, whereas the latter only achieves accuracy $\frac1{2}+\varepsilon$. We then show, through extensive experiments, that Top-$k$ outperforms the two main approaches to decision tree learning: classic greedy algorithms and more recent "optimal decision tree" algorithms. On one hand, Top-$k$ consistently enjoys significant accuracy gains over greedy algorithms across a wide range of benchmarks. On the other hand, Top-$k$ is markedly more scalable than optimal decision tree algorithms and is able to handle dataset and feature set sizes that remain far beyond the reach of these algorithms.

MAPTree: Beating "Optimal" Decision Trees with Bayesian Decision Trees

Decision trees remain one of the most popular machine learning models today, largely due to their out-of-the-box performance and interpretability. In this work, we present a Bayesian approach to decision tree induction via maximum a posteriori inference of a posterior distribution over trees. We first demonstrate a connection between maximum a posteriori inference of decision trees and AND/OR search. Using this connection, we propose an AND/OR search algorithm, dubbed MAPTree, which is able to recover the maximum a posteriori tree. Lastly, we demonstrate the empirical performance of the maximum a posteriori tree both on synthetic data and in real world settings. On 16 real world datasets, MAPTree either outperforms baselines or demonstrates comparable performance but with much smaller trees. On a synthetic dataset, MAPTree also demonstrates greater robustness to noise and better generalization than existing approaches. Finally, MAPTree recovers the maxiumum a posteriori tree faster than existing sampling approaches and, in contrast with those algorithms, is able to provide a certificate of optimality. The code for our experiments is available at https://github.com/ThrunGroup/maptree.

Accelerating Machine Learning Algorithms with Adaptive Sampling

The era of huge data necessitates highly efficient machine learning algorithms. Many common machine learning algorithms, however, rely on computationally intensive subroutines that are prohibitively expensive on large datasets. Oftentimes, existing techniques subsample the data or use other methods to improve computational efficiency, at the expense of incurring some approximation error. This thesis demonstrates that it is often sufficient, instead, to substitute computationally intensive subroutines with a special kind of randomized counterparts that results in almost no degradation in quality.

Bayesian Decision Trees via Tractable Priors and Probabilistic Context-Free Grammars

Decision Trees are some of the most popular machine learning models today due to their out-of-the-box performance and interpretability. Often, Decision Trees models are constructed greedily in a top-down fashion via heuristic search criteria, such as Gini impurity or entropy. However, trees constructed in this manner are sensitive to minor fluctuations in training data and are prone to overfitting. In contrast, Bayesian approaches to tree construction formulate the selection process as a posterior inference problem; such approaches are more stable and provide greater theoretical guarantees. However, generating Bayesian Decision Trees usually requires sampling from complex, multimodal posterior distributions. Current Markov Chain Monte Carlo-based approaches for sampling Bayesian Decision Trees are prone to mode collapse and long mixing times, which makes them impractical. In this paper, we propose a new criterion for training Bayesian Decision Trees. Our criterion gives rise to BCART-PCFG, which can efficiently sample decision trees from a posterior distribution across trees given the data and find the maximum a posteriori (MAP) tree. Learning the posterior and training the sampler can be done in time that is polynomial in the dataset size. Once the posterior has been learned, trees can be sampled efficiently (linearly in the number of nodes). At the core of our method is a reduction of sampling the posterior to sampling a derivation from a probabilistic context-free grammar. We find that trees sampled via BCART-PCFG perform comparable to or better than greedily-constructed Decision Trees in classification accuracy on several datasets. Additionally, the trees sampled via BCART-PCFG are significantly smaller -- sometimes by as much as 20x.

Faster Maximum Inner Product Search in High Dimensions

Maximum Inner Product Search (MIPS) is a popular problem in the machine learning literature due to its applicability in a wide array of applications, such as recommender systems. In high-dimensional settings, however, MIPS queries can become computationally expensive as most existing solutions do not scale well with data dimensionality. In this work, we present a state-of-the-art algorithm for the MIPS problem in high dimensions, dubbed BanditMIPS. BanditMIPS is a randomized algorithm that borrows techniques from multi-armed bandits to reduce the MIPS problem to a best-arm identification problem. BanditMIPS reduces the complexity of state-of-the-art algorithms from $O(\sqrt{d})$ to $O(\text{log}d)$, where $d$ is the dimension of the problem data vectors. On high-dimensional real-world datasets, BanditMIPS runs approximately 12 times faster than existing approaches and returns the same solution. BanditMIPS requires no preprocessing of the data and includes a hyperparameter that practitioners may use to trade off accuracy and runtime. We also propose a variant of our algorithm, named BanditMIPS-$\alpha$, which employs non-uniform sampling across the data dimensions to provide further speedups.

MABSplit: Faster Forest Training Using Multi-Armed Bandits

Random forests are some of the most widely used machine learning models today, especially in domains that necessitate interpretability. We present an algorithm that accelerates the training of random forests and other popular tree-based learning methods. At the core of our algorithm is a novel node-splitting subroutine, dubbed MABSplit, used to efficiently find split points when constructing decision trees. Our algorithm borrows techniques from the multi-armed bandit literature to judiciously determine how to allocate samples and computational power across candidate split points. We provide theoretical guarantees that MABSplit improves the sample complexity of each node split from linear to logarithmic in the number of data points. In some settings, MABSplit leads to 100x faster training (an 99% reduction in training time) without any decrease in generalization performance. We demonstrate similar speedups when MABSplit is used across a variety of forest-based variants, such as Extremely Random Forests and Random Patches. We also show our algorithm can be used in both classification and regression tasks. Finally, we show that MABSplit outperforms existing methods in generalization performance and feature importance calculations under a fixed computational budget. All of our experimental results are reproducible via a one-line script at https://github.com/ThrunGroup/FastForest.