LeanAgent: Lifelong Learning for Formal Theorem Proving

Large Language Models (LLMs) have been successful in mathematical reasoning tasks such as formal theorem proving when integrated with interactive proof assistants like Lean. Existing approaches involve training or fine-tuning an LLM on a specific dataset to perform well on particular domains, such as undergraduate-level mathematics. These methods struggle with generalizability to advanced mathematics. A fundamental limitation is that these approaches operate on static domains, failing to capture how mathematicians often work across multiple domains and projects simultaneously or cyclically. We present LeanAgent, a novel lifelong learning framework for theorem proving that continuously generalizes to and improves on ever-expanding mathematical knowledge without forgetting previously learned knowledge. LeanAgent introduces several key innovations, including a curriculum learning strategy that optimizes the learning trajectory in terms of mathematical difficulty, a dynamic database for efficient management of evolving mathematical knowledge, and progressive training to balance stability and plasticity. LeanAgent successfully proves 162 theorems previously unproved by humans across 23 diverse Lean repositories, many from advanced mathematics. It performs up to 11$\times$ better than the static LLM baseline, proving challenging theorems in domains like abstract algebra and algebraic topology while showcasing a clear progression of learning from basic concepts to advanced topics. In addition, we analyze LeanAgent's superior performance on key lifelong learning metrics. LeanAgent achieves exceptional scores in stability and backward transfer, where learning new tasks improves performance on previously learned tasks. This emphasizes LeanAgent's continuous generalizability and improvement, explaining its superior theorem proving performance.

Creative and Context-Aware Translation of East Asian Idioms with GPT-4

As a type of figurative language, an East Asian idiom condenses rich cultural background into only a few characters. Translating such idioms is challenging for human translators, who often resort to choosing a context-aware translation from an existing list of candidates. However, compiling a dictionary of candidate translations demands much time and creativity even for expert translators. To alleviate such burden, we evaluate if GPT-4 can help generate high-quality translations. Based on automatic evaluations of faithfulness and creativity, we first identify Pareto-optimal prompting strategies that can outperform translation engines from Google and DeepL. Then, at a low cost, our context-aware translations can achieve far more high-quality translations per idiom than the human baseline. We open-source all code and data to facilitate further research.

Towards Large Language Models as Copilots for Theorem Proving in Lean

Theorem proving is an important challenge for large language models (LLMs), as formal proofs can be checked rigorously by proof assistants such as Lean, leaving no room for hallucination. Existing LLM-based provers try to prove theorems in a fully autonomous mode without human intervention. In this mode, they struggle with novel and challenging theorems, for which human insights may be critical. In this paper, we explore LLMs as copilots that assist humans in proving theorems. We introduce Lean Copilot, a framework for running LLM inference in Lean. It enables programmers to build various LLM-based proof automation tools that integrate seamlessly into the workflow of Lean users. Using Lean Copilot, we build tools for suggesting proof steps (tactic suggestion), completing intermediate proof goals (proof search), and selecting relevant premises (premise selection) using LLMs. Users can use our pretrained models or bring their own ones that run either locally (with or without GPUs) or on the cloud. Experimental results demonstrate the effectiveness of our method in assisting humans and automating theorem proving process compared to existing rule-based proof automation in Lean. We open source all codes under a permissive MIT license to facilitate further research.

LeanDojo: Theorem Proving with Retrieval-Augmented Language Models

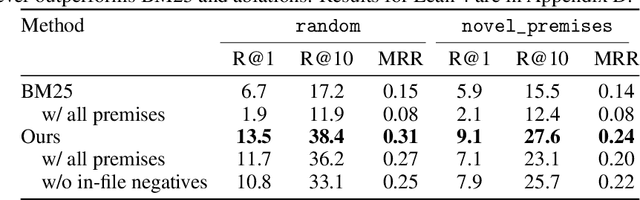
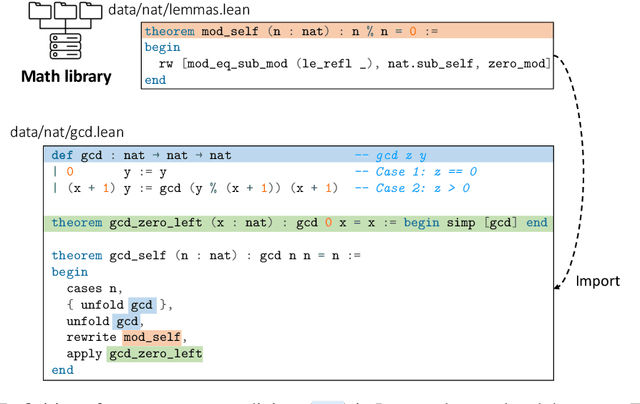
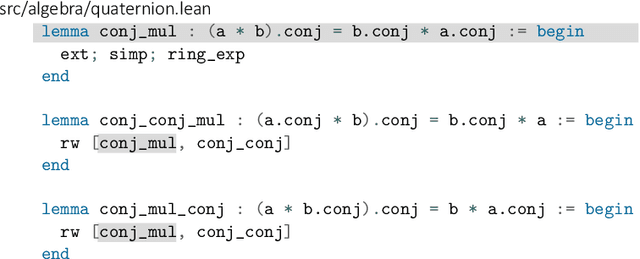
Large language models (LLMs) have shown promise in proving formal theorems using proof assistants such as Lean. However, existing methods are difficult to reproduce or build on, due to private code, data, and large compute requirements. This has created substantial barriers to research on machine learning methods for theorem proving. This paper removes these barriers by introducing LeanDojo: an open-source Lean playground consisting of toolkits, data, models, and benchmarks. LeanDojo extracts data from Lean and enables interaction with the proof environment programmatically. It contains fine-grained annotations of premises in proofs, providing valuable data for premise selection: a key bottleneck in theorem proving. Using this data, we develop ReProver (Retrieval-Augmented Prover): the first LLM-based prover that is augmented with retrieval for selecting premises from a vast math library. It is inexpensive and needs only one GPU week of training. Our retriever leverages LeanDojo's program analysis capability to identify accessible premises and hard negative examples, which makes retrieval much more effective. Furthermore, we construct a new benchmark consisting of 96,962 theorems and proofs extracted from Lean's math library. It features challenging data split requiring the prover to generalize to theorems relying on novel premises that are never used in training. We use this benchmark for training and evaluation, and experimental results demonstrate the effectiveness of ReProver over non-retrieval baselines and GPT-4. We thus provide the first set of open-source LLM-based theorem provers without any proprietary datasets and release it under a permissive MIT license to facilitate further research.

For a Higher Capacity: The Combination of FTN and NOMA Technologies in SC and MIMO Scenarios

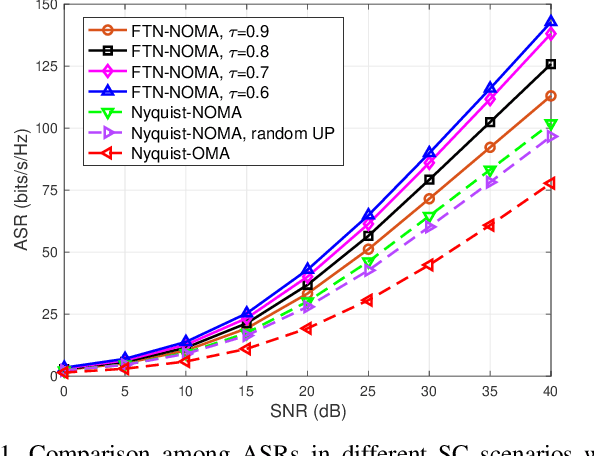
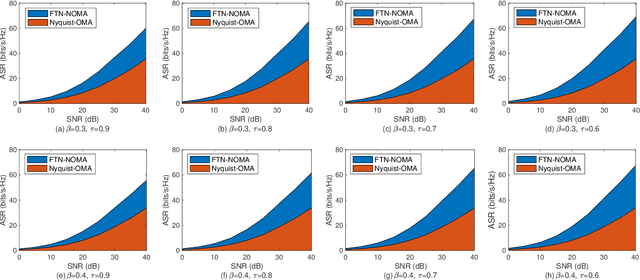
The development of the industrial Internet of Things (IoT) calls for higher spectrum efficiency (SE). Faster than Nyquist (FTN) and non-orthogonal multiple access (NOMA) are both promising paradigms to improve the SE without any extra spectrum resources required. The combination of FTN and NOMA is an interesting issue and has been focused on recently. In the NOMA technology, user pairing and power allocation are key algorithms determining system capacity. This paper first proposes a joint user pairing and power allocation algorithm for the FTN-based single-carrier (SC) NOMA system. Then, the FTN-based multiple-input-multiple-output (MIMO) NOMA is studied and a dynamic user pairing and power allocation scheme is presented. In both scenarios, the maximum available sum rate (ASR) is the target. While based on the fairness principle, the user's SE in the NOMA system is guaranteed to be no less than that in the OMA system. Simulation results show the advantage of the FTN-based NOMA with the proposed scheme in ASR and quality of service (QoS) performance. As far as we know, this paper is the first solution to the issue of user pairing and power allocation in FTN-based NOMA, which proves the great advantage of the combination of these two state-of-the-art technologies.