Haydn Maust
Fourier Continuation for Exact Derivative Computation in Physics-Informed Neural Operators
Nov 29, 2022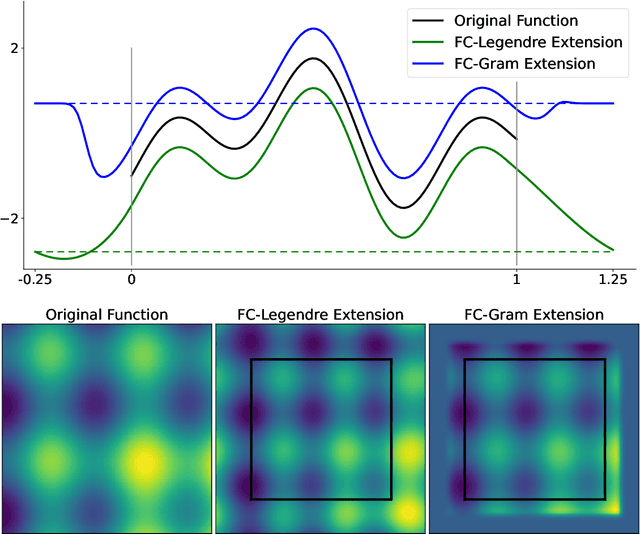

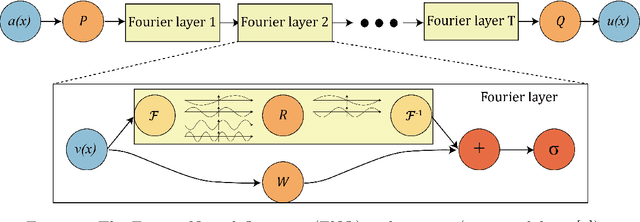
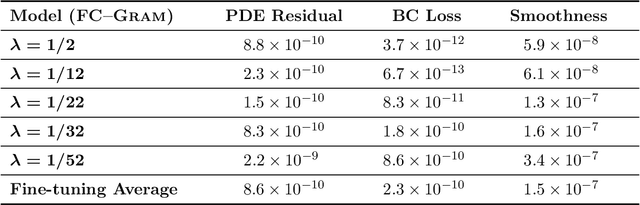
Abstract:The physics-informed neural operator (PINO) is a machine learning architecture that has shown promising empirical results for learning partial differential equations. PINO uses the Fourier neural operator (FNO) architecture to overcome the optimization challenges often faced by physics-informed neural networks. Since the convolution operator in PINO uses the Fourier series representation, its gradient can be computed exactly on the Fourier space. While Fourier series cannot represent nonperiodic functions, PINO and FNO still have the expressivity to learn nonperiodic problems with Fourier extension via padding. However, computing the Fourier extension in the physics-informed optimization requires solving an ill-conditioned system, resulting in inaccurate derivatives which prevent effective optimization. In this work, we present an architecture that leverages Fourier continuation (FC) to apply the exact gradient method to PINO for nonperiodic problems. This paper investigates three different ways that FC can be incorporated into PINO by testing their performance on a 1D blowup problem. Experiments show that FC-PINO outperforms padded PINO, improving equation loss by several orders of magnitude, and it can accurately capture the third order derivatives of nonsmooth solution functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge