Ambient Noise Full Waveform Inversion with Neural Operators

Numerical simulations of seismic wave propagation are crucial for investigating velocity structures and improving seismic hazard assessment. However, standard methods such as finite difference or finite element are computationally expensive. Recent studies have shown that a new class of machine learning models, called neural operators, can solve the elastodynamic wave equation orders of magnitude faster than conventional methods. Full waveform inversion is a prime beneficiary of the accelerated simulations. Neural operators, as end-to-end differentiable operators, combined with automatic differentiation, provide an alternative approach to the adjoint-state method. Since neural operators do not involve the Born approximation, when used for full waveform inversion they have the potential to include additional phases and alleviate cycle-skipping problems present in traditional adjoint-state formulations. In this study, we demonstrate the application of neural operators for full waveform inversion on a real seismic dataset, which consists of several nodal transects collected across the San Gabriel, Chino, and San Bernardino basins in the Los Angeles metropolitan area.

Seismic wave propagation and inversion with Neural Operators

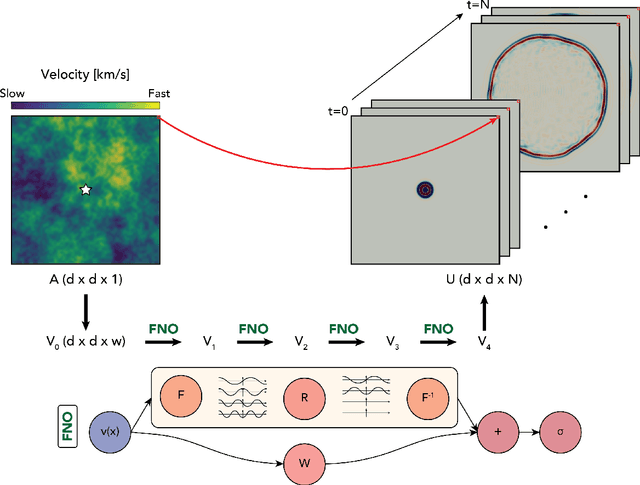
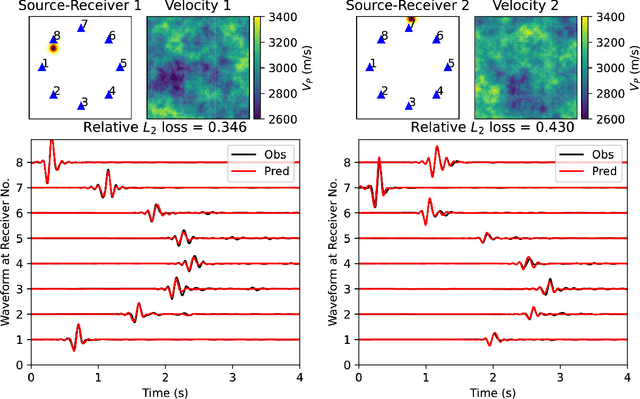
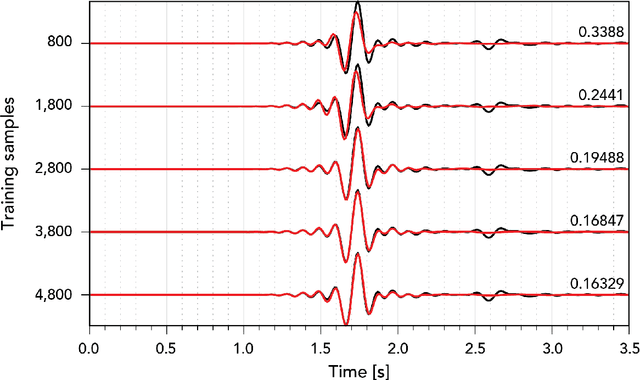
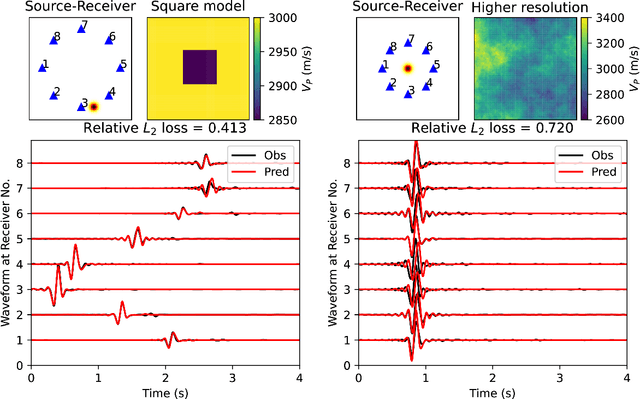
Seismic wave propagation forms the basis for most aspects of seismological research, yet solving the wave equation is a major computational burden that inhibits the progress of research. This is exaspirated by the fact that new simulations must be performed when the velocity structure or source location is perturbed. Here, we explore a prototype framework for learning general solutions using a recently developed machine learning paradigm called Neural Operator. A trained Neural Operator can compute a solution in negligible time for any velocity structure or source location. We develop a scheme to train Neural Operators on an ensemble of simulations performed with random velocity models and source locations. As Neural Operators are grid-free, it is possible to evaluate solutions on higher resolution velocity models than trained on, providing additional computational efficiency. We illustrate the method with the 2D acoustic wave equation and demonstrate the method's applicability to seismic tomography, using reverse mode automatic differentiation to compute gradients of the wavefield with respect to the velocity structure. The developed procedure is nearly an order of magnitude faster than using conventional numerical methods for full waveform inversion.

Extracting dispersion curves from ambient noise correlations using deep learning

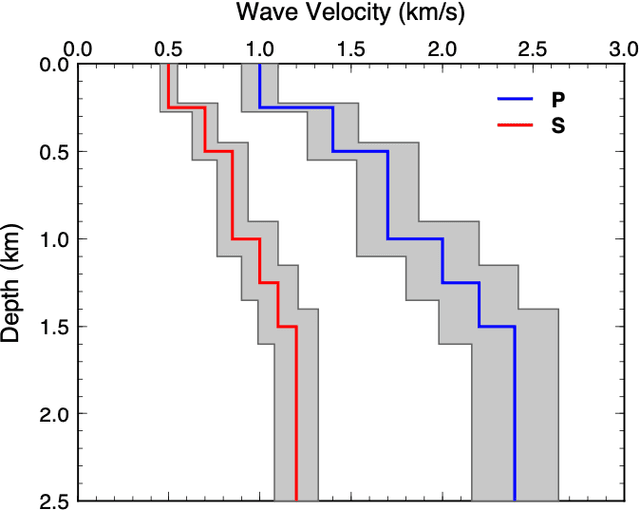
We present a machine-learning approach to classifying the phases of surface wave dispersion curves. Standard FTAN analysis of surfaces observed on an array of receivers is converted to an image, of which, each pixel is classified as fundamental mode, first overtone, or noise. We use a convolutional neural network (U-net) architecture with a supervised learning objective and incorporate transfer learning. The training is initially performed with synthetic data to learn coarse structure, followed by fine-tuning of the network using approximately 10% of the real data based on human classification. The results show that the machine classification is nearly identical to the human picked phases. Expanding the method to process multiple images at once did not improve the performance. The developed technique will faciliate automated processing of large dispersion curve datasets.