HypoSVI: Hypocenter inversion with Stein variational inference and Physics Informed Neural Networks

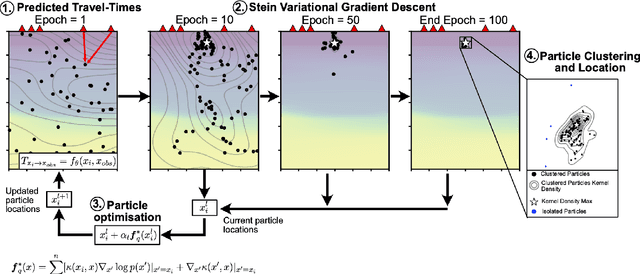
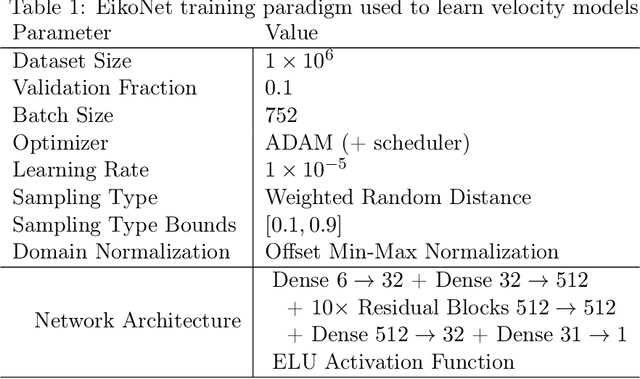
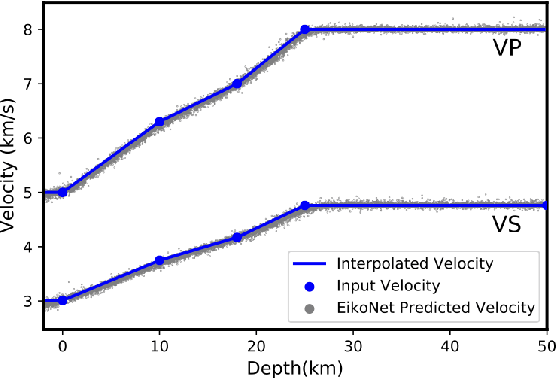
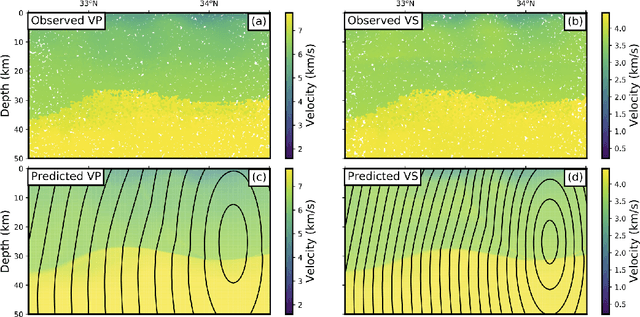
We introduce a scheme for probabilistic hypocenter inversion with Stein variational inference. Our approach uses a differentiable forward model in the form of a physics-informed neural network, which we train to solve the Eikonal equation. This allows for rapid approximation of the posterior by iteratively optimizing a collection of particles against a kernelized Stein discrepancy. We show that the method is well-equipped to handle highly non-convex posterior distributions, which are common in hypocentral inverse problems. A suite of experiments is performed to examine the influence of the various hyperparameters. Once trained, the method is valid for any network geometry within the study area without the need to build travel time tables. We show that the computational demands scale efficiently with the number of differential times, making it ideal for large-N sensing technologies like Distributed Acoustic Sensing.