Principled Probabilistic Imaging using Diffusion Models as Plug-and-Play Priors
Paper and Code
May 29, 2024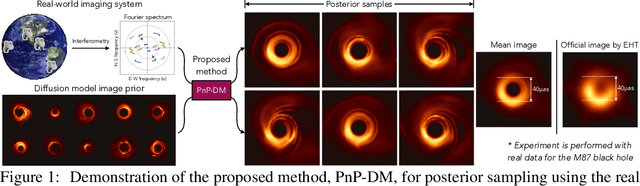
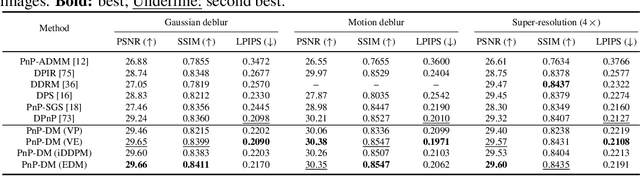
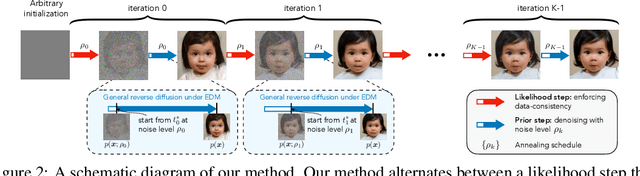

Diffusion models (DMs) have recently shown outstanding capability in modeling complex image distributions, making them expressive image priors for solving Bayesian inverse problems. However, most existing DM-based methods rely on approximations in the generative process to be generic to different inverse problems, leading to inaccurate sample distributions that deviate from the target posterior defined within the Bayesian framework. To harness the generative power of DMs while avoiding such approximations, we propose a Markov chain Monte Carlo algorithm that performs posterior sampling for general inverse problems by reducing it to sampling the posterior of a Gaussian denoising problem. Crucially, we leverage a general DM formulation as a unified interface that allows for rigorously solving the denoising problem with a range of state-of-the-art DMs. We demonstrate the effectiveness of the proposed method on six inverse problems (three linear and three nonlinear), including a real-world black hole imaging problem. Experimental results indicate that our proposed method offers more accurate reconstructions and posterior estimation compared to existing DM-based imaging inverse methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge