Towards an Algebraic Framework For Approximating Functions Using Neural Network Polynomials

We make the case for neural network objects and extend an already existing neural network calculus explained in detail in Chapter 2 on \cite{bigbook}. Our aim will be to show that, yes, indeed, it makes sense to talk about neural network polynomials, neural network exponentials, sine, and cosines in the sense that they do indeed approximate their real number counterparts subject to limitations on certain of their parameters, $q$, and $\varepsilon$. While doing this, we show that the parameter and depth growth are only polynomial on their desired accuracy (defined as a 1-norm difference over $\mathbb{R}$), thereby showing that this approach to approximating, where a neural network in some sense has the structural properties of the function it is approximating is not entire intractable.

Self-Learned Kernel Low Rank Approach TO Accelerated High Resolution 3D Diffusion MRI

Diffusion Magnetic Resonance Imaging (dMRI) is a promising method to analyze the subtle changes in the tissue structure. However, the lengthy acquisition time is a major limitation in the clinical application of dMRI. Different image acquisition techniques such as parallel imaging, compressed sensing, has shortened the prolonged acquisition time but creating high-resolution 3D dMRI slices still requires a significant amount of time. In this study, we have shown that high-resolution 3D dMRI can be reconstructed from the highly undersampled k-space and q-space data using a Kernel LowRank method. Our proposed method has outperformed the conventional CS methods in terms of both image quality and diffusion maps constructed from the diffusion-weighted images

Spectral Decomposition in Deep Networks for Segmentation of Dynamic Medical Images

Dynamic contrast-enhanced magnetic resonance imaging (DCE- MRI) is a widely used multi-phase technique routinely used in clinical practice. DCE and similar datasets of dynamic medical data tend to contain redundant information on the spatial and temporal components that may not be relevant for detection of the object of interest and result in unnecessarily complex computer models with long training times that may also under-perform at test time due to the abundance of noisy heterogeneous data. This work attempts to increase the training efficacy and performance of deep networks by determining redundant information in the spatial and spectral components and show that the performance of segmentation accuracy can be maintained and potentially improved. Reported experiments include the evaluation of training/testing efficacy on a heterogeneous dataset composed of abdominal images of pediatric DCE patients, showing that drastic data reduction (higher than 80%) can preserve the dynamic information and performance of the segmentation model, while effectively suppressing noise and unwanted portion of the images.

Kernel Bi-Linear Modeling for Reconstructing Data on Manifolds: The Dynamic-MRI Case

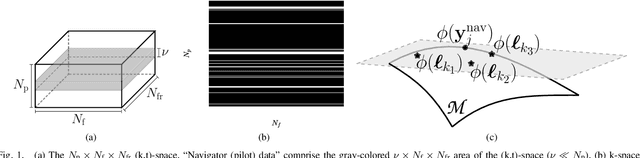
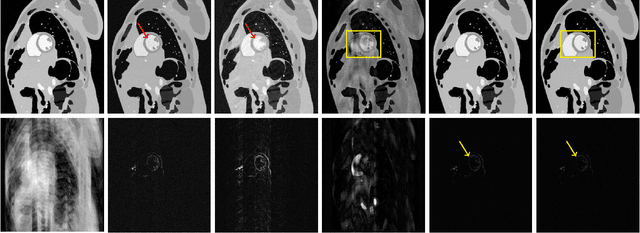
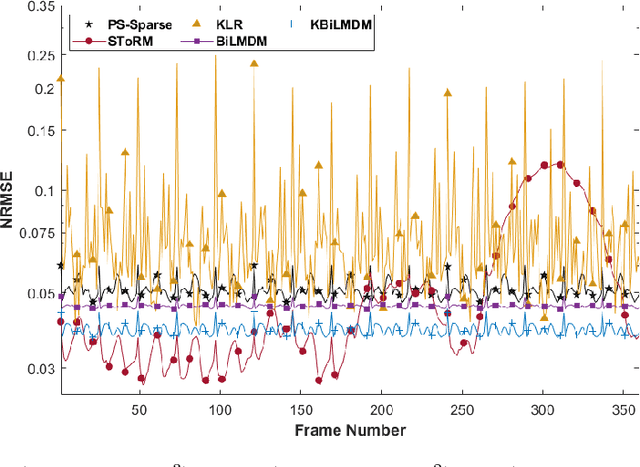
This paper establishes a kernel-based framework for reconstructing data on manifolds, tailored to fit the dynamic-(d)MRI-data recovery problem. The proposed methodology exploits simple tangent-space geometries of manifolds in reproducing kernel Hilbert spaces and follows classical kernel-approximation arguments to form the data-recovery task as a bi-linear inverse problem. Departing from mainstream approaches, the proposed methodology uses no training data, employs no graph Laplacian matrix to penalize the optimization task, uses no costly (kernel) pre-imaging step to map feature points back to the input space, and utilizes complex-valued kernel functions to account for k-space data. The framework is validated on synthetically generated dMRI data, where comparisons against state-of-the-art schemes highlight the rich potential of the proposed approach in data-recovery problems.

Diagnostic Image Quality Assessment and Classification in Medical Imaging: Opportunities and Challenges

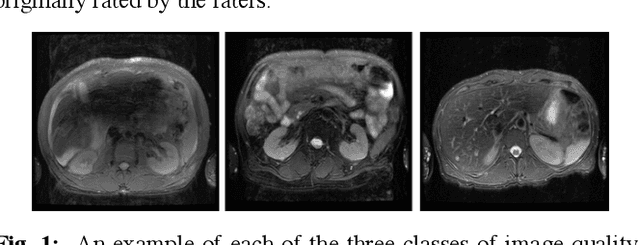
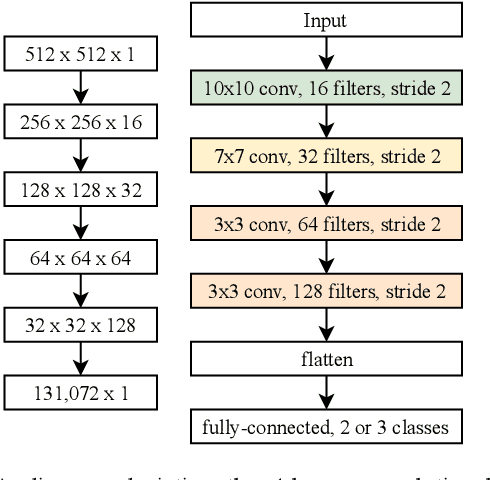
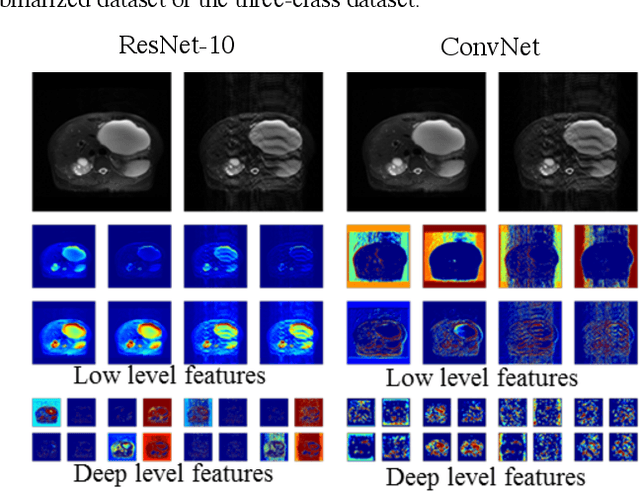
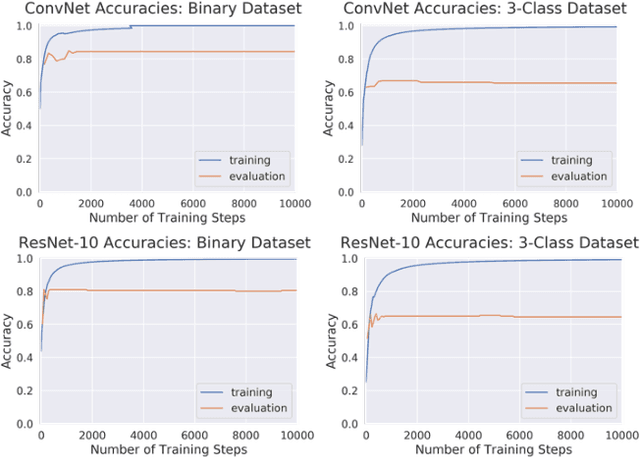
Magnetic Resonance Imaging (MRI) suffers from several artifacts, the most common of which are motion artifacts. These artifacts often yield images that are of non-diagnostic quality. To detect such artifacts, images are prospectively evaluated by experts for their diagnostic quality, which necessitates patient-revisits and rescans whenever non-diagnostic quality scans are encountered. This motivates the need to develop an automated framework capable of accessing medical image quality and detecting diagnostic and non-diagnostic images. In this paper, we explore several convolutional neural network-based frameworks for medical image quality assessment and investigate several challenges therein.

Bi-Linear Modeling of Data Manifolds for Dynamic-MRI Recovery

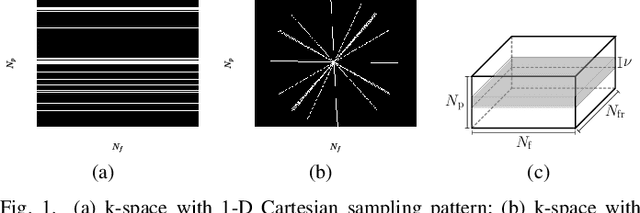
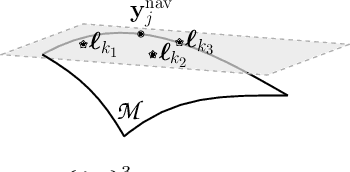
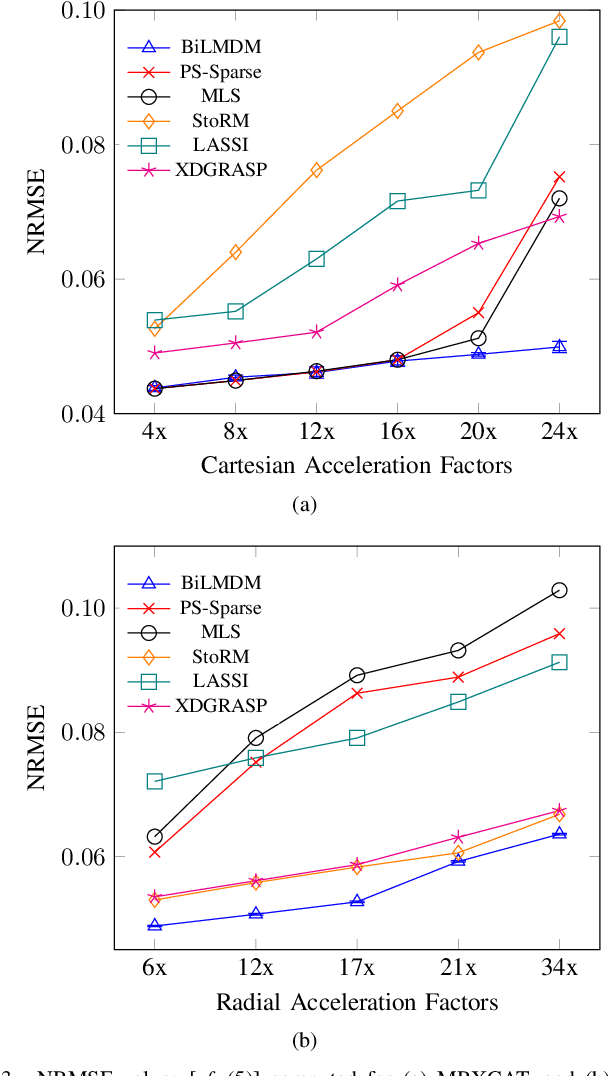
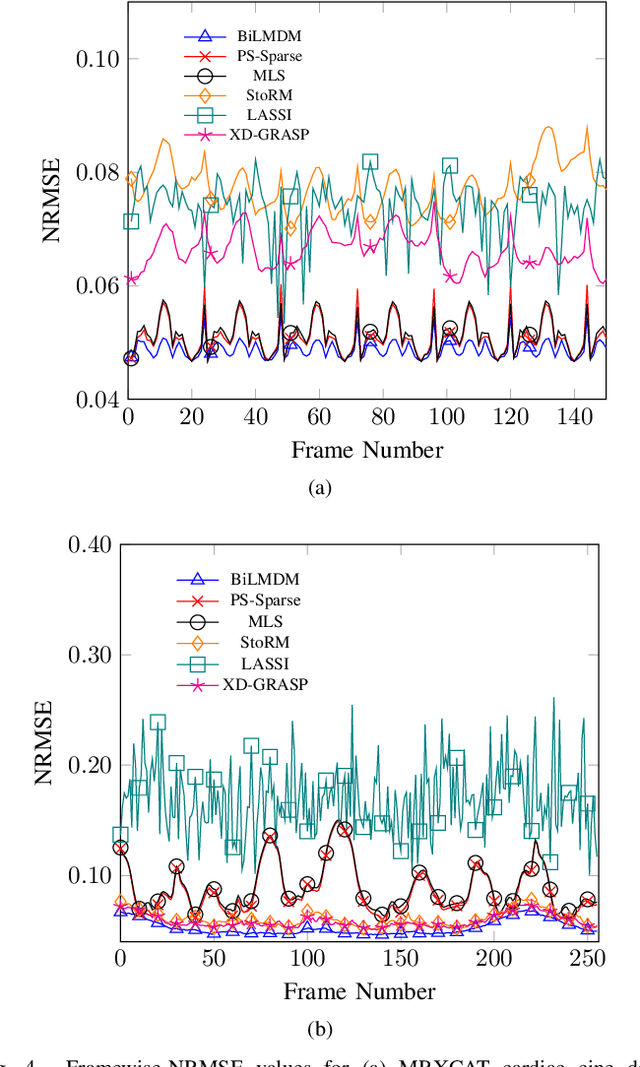
This paper puts forth a novel bi-linear modeling framework for data recovery via manifold-learning and sparse-approximation arguments and considers its application to dynamic magnetic-resonance imaging (dMRI). Each temporal-domain MR image is viewed as a point that lies onto or close to a smooth manifold, and landmark points are identified to describe the point cloud concisely. To facilitate computations, a dimensionality reduction module generates low-dimensional/compressed renditions of the landmark points. Recovery of the high-fidelity MRI data is realized by solving a non-convex minimization task for the linear decompression operator and those affine combinations of landmark points which locally approximate the latent manifold geometry. An algorithm with guaranteed convergence to stationary solutions of the non-convex minimization task is also provided. The aforementioned framework exploits the underlying spatio-temporal patterns and geometry of the acquired data without any prior training on external data or information. Extensive numerical results on simulated as well as real cardiac-cine and perfusion MRI data illustrate noteworthy improvements of the advocated machine-learning framework over state-of-the-art reconstruction techniques.