Kernel Bi-Linear Modeling for Reconstructing Data on Manifolds: The Dynamic-MRI Case

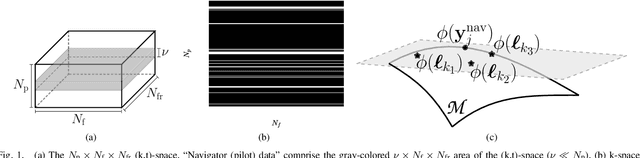
This paper establishes a kernel-based framework for reconstructing data on manifolds, tailored to fit the dynamic-(d)MRI-data recovery problem. The proposed methodology exploits simple tangent-space geometries of manifolds in reproducing kernel Hilbert spaces and follows classical kernel-approximation arguments to form the data-recovery task as a bi-linear inverse problem. Departing from mainstream approaches, the proposed methodology uses no training data, employs no graph Laplacian matrix to penalize the optimization task, uses no costly (kernel) pre-imaging step to map feature points back to the input space, and utilizes complex-valued kernel functions to account for k-space data. The framework is validated on synthetically generated dMRI data, where comparisons against state-of-the-art schemes highlight the rich potential of the proposed approach in data-recovery problems.

Bi-Linear Modeling of Data Manifolds for Dynamic-MRI Recovery

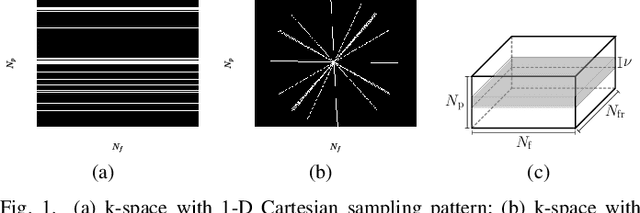
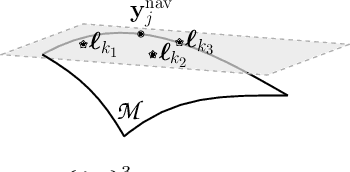
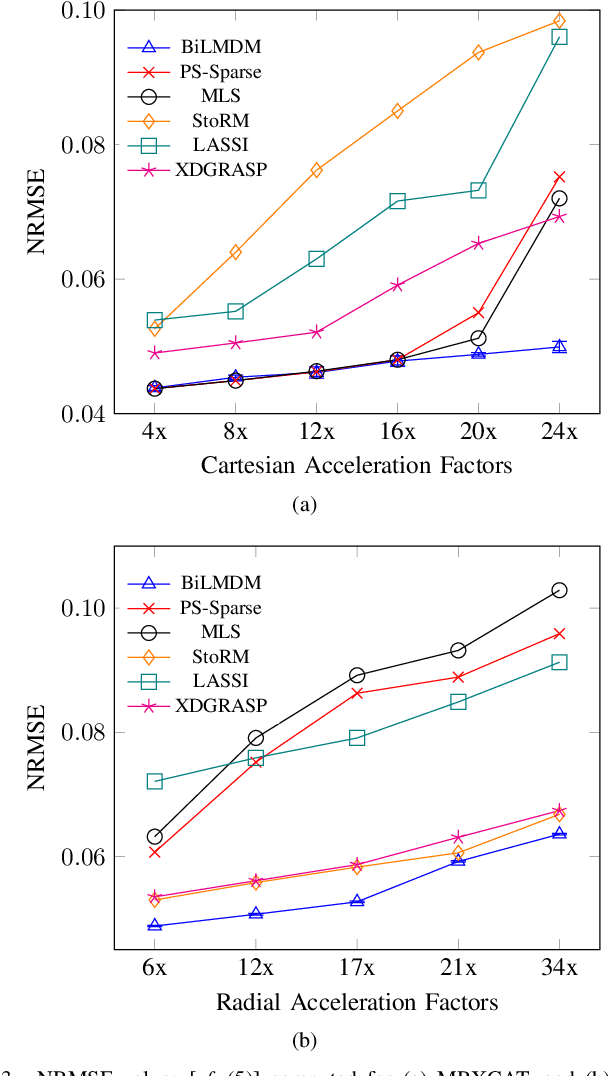
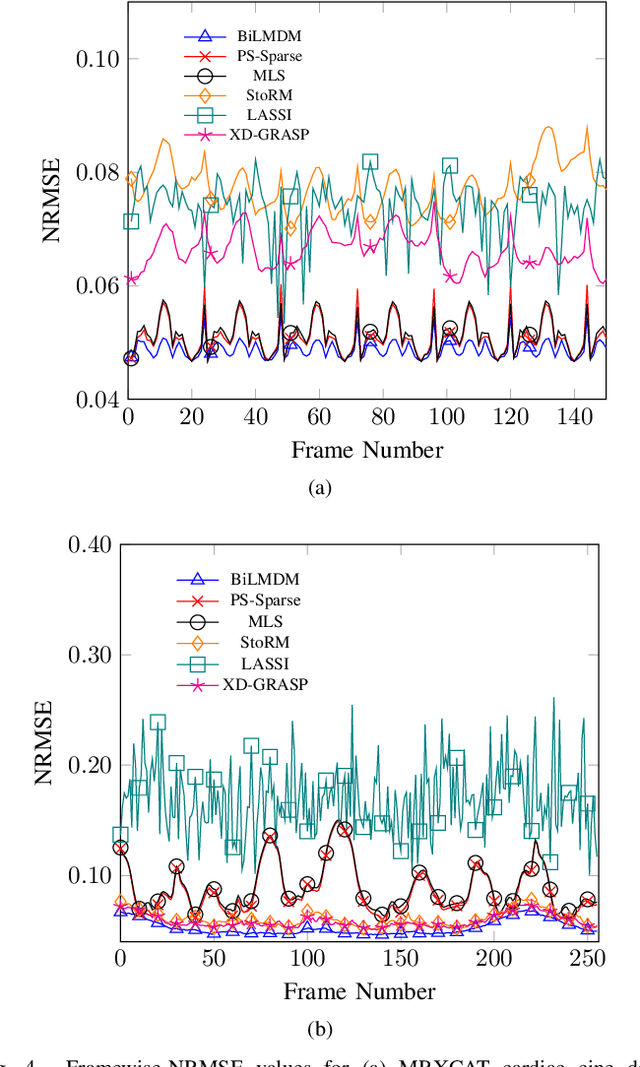
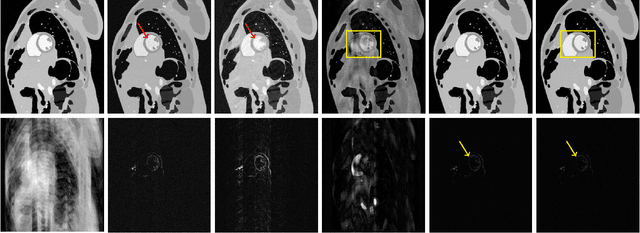
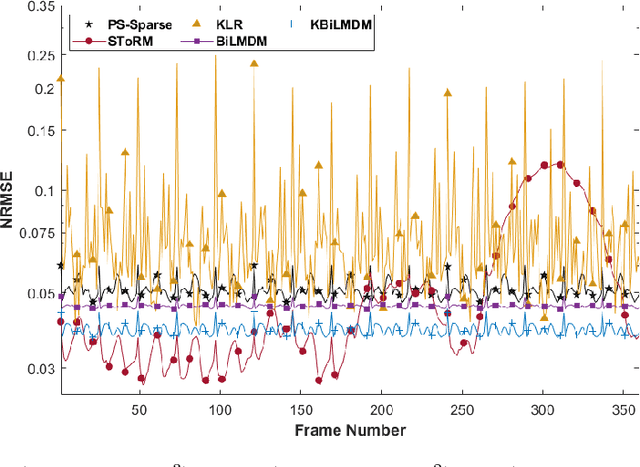
This paper puts forth a novel bi-linear modeling framework for data recovery via manifold-learning and sparse-approximation arguments and considers its application to dynamic magnetic-resonance imaging (dMRI). Each temporal-domain MR image is viewed as a point that lies onto or close to a smooth manifold, and landmark points are identified to describe the point cloud concisely. To facilitate computations, a dimensionality reduction module generates low-dimensional/compressed renditions of the landmark points. Recovery of the high-fidelity MRI data is realized by solving a non-convex minimization task for the linear decompression operator and those affine combinations of landmark points which locally approximate the latent manifold geometry. An algorithm with guaranteed convergence to stationary solutions of the non-convex minimization task is also provided. The aforementioned framework exploits the underlying spatio-temporal patterns and geometry of the acquired data without any prior training on external data or information. Extensive numerical results on simulated as well as real cardiac-cine and perfusion MRI data illustrate noteworthy improvements of the advocated machine-learning framework over state-of-the-art reconstruction techniques.