On the Impossibility of Global Convergence in Multi-Loss Optimization

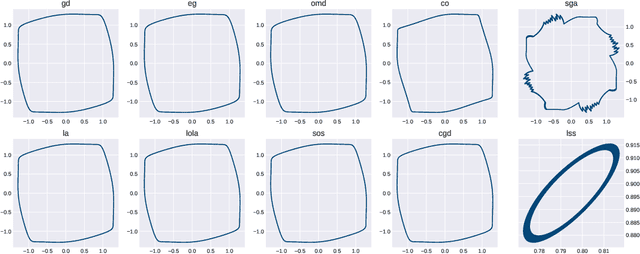
Under mild regularity conditions, gradient-based methods converge globally to a critical point in the single-loss setting. This is known to break down for vanilla gradient descent when moving to multi-loss optimization, but can we hope to build some algorithm with global guarantees? We negatively resolve this open problem by proving that any reasonable algorithm will exhibit limit cycles or diverge to infinite losses in some differentiable game, even in two-player games with zero-sum interactions. A reasonable algorithm is simply one which avoids strict maxima, an exceedingly weak assumption since converging to maxima would be the opposite of minimization. This impossibility theorem holds even if we impose existence of a strict minimum and no other critical points. The proof is constructive, enabling us to display explicit limit cycles for existing gradient-based methods. Nonetheless, it remains an open question whether cycles arise in high-dimensional games of interest to ML practitioners, such as GANs or multi-agent RL.