From Restless to Contextual: A Thresholding Bandit Approach to Improve Finite-horizon Performance
Paper and Code
Feb 07, 2025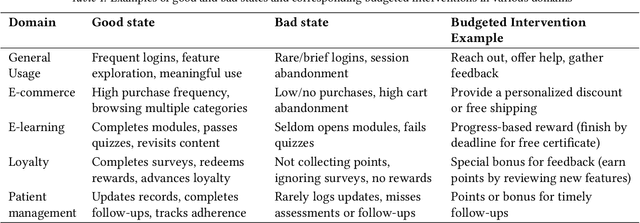
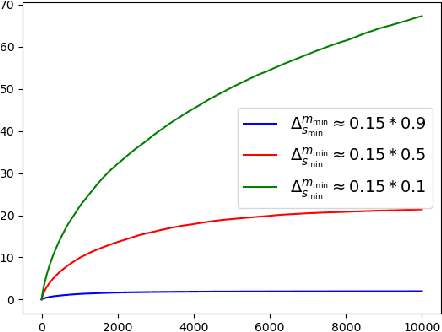
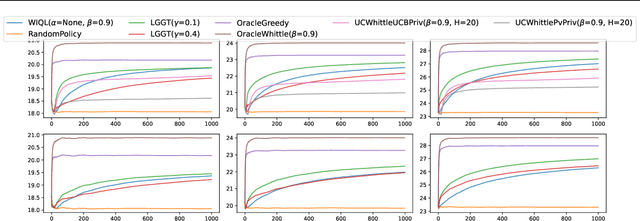
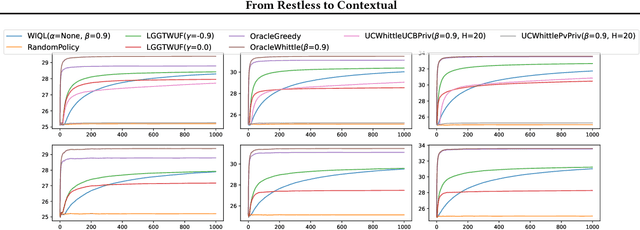
Online restless bandits extend classic contextual bandits by incorporating state transitions and budget constraints, representing each agent as a Markov Decision Process (MDP). This framework is crucial for finite-horizon strategic resource allocation, optimizing limited costly interventions for long-term benefits. However, learning the underlying MDP for each agent poses a major challenge in finite-horizon settings. To facilitate learning, we reformulate the problem as a scalable budgeted thresholding contextual bandit problem, carefully integrating the state transitions into the reward design and focusing on identifying agents with action benefits exceeding a threshold. We establish the optimality of an oracle greedy solution in a simple two-state setting, and propose an algorithm that achieves minimax optimal constant regret in the online multi-state setting with heterogeneous agents and knowledge of outcomes under no intervention. We numerically show that our algorithm outperforms existing online restless bandit methods, offering significant improvements in finite-horizon performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge