Reward Maximization for Pure Exploration: Minimax Optimal Good Arm Identification for Nonparametric Multi-Armed Bandits
Paper and Code
Oct 21, 2024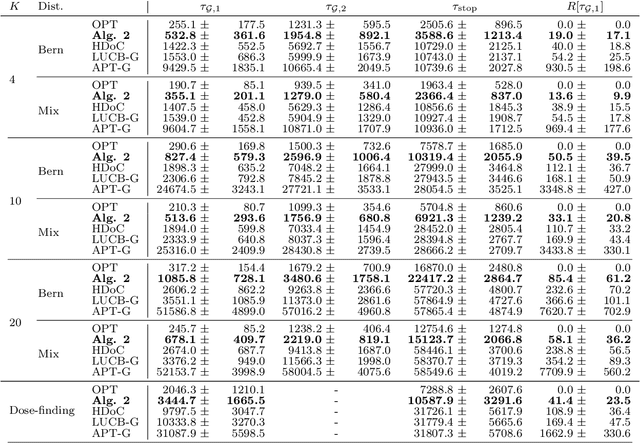
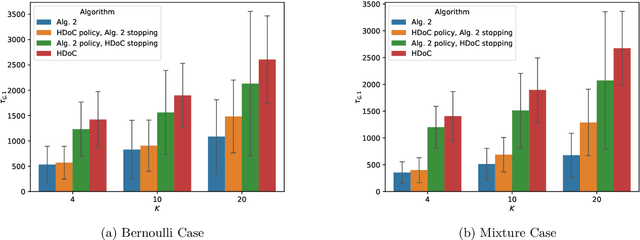
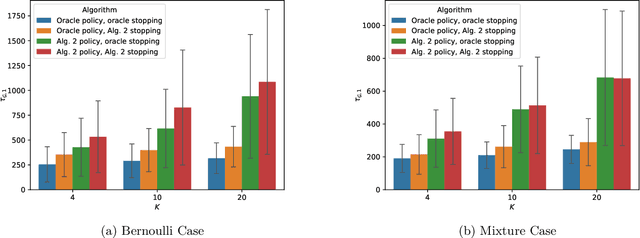

In multi-armed bandits, the tasks of reward maximization and pure exploration are often at odds with each other. The former focuses on exploiting arms with the highest means, while the latter may require constant exploration across all arms. In this work, we focus on good arm identification (GAI), a practical bandit inference objective that aims to label arms with means above a threshold as quickly as possible. We show that GAI can be efficiently solved by combining a reward-maximizing sampling algorithm with a novel nonparametric anytime-valid sequential test for labeling arm means. We first establish that our sequential test maintains error control under highly nonparametric assumptions and asymptotically achieves the minimax optimal e-power, a notion of power for anytime-valid tests. Next, by pairing regret-minimizing sampling schemes with our sequential test, we provide an approach that achieves minimax optimal stopping times for labeling arms with means above a threshold, under an error probability constraint. Our empirical results validate our approach beyond the minimax setting, reducing the expected number of samples for all stopping times by at least 50% across both synthetic and real-world settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge