Embrace the Gap: VAEs Perform Independent Mechanism Analysis
Paper and Code
Jun 06, 2022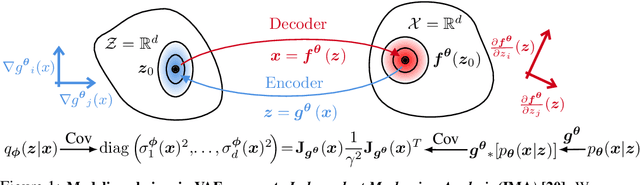

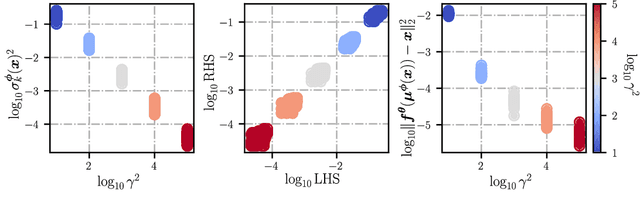

Variational autoencoders (VAEs) are a popular framework for modeling complex data distributions; they can be efficiently trained via variational inference by maximizing the evidence lower bound (ELBO), at the expense of a gap to the exact (log-)marginal likelihood. While VAEs are commonly used for representation learning, it is unclear why ELBO maximization would yield useful representations, since unregularized maximum likelihood estimation cannot invert the data-generating process. Yet, VAEs often succeed at this task. We seek to elucidate this apparent paradox by studying nonlinear VAEs in the limit of near-deterministic decoders. We first prove that, in this regime, the optimal encoder approximately inverts the decoder -- a commonly used but unproven conjecture -- which we refer to as {\em self-consistency}. Leveraging self-consistency, we show that the ELBO converges to a regularized log-likelihood. This allows VAEs to perform what has recently been termed independent mechanism analysis (IMA): it adds an inductive bias towards decoders with column-orthogonal Jacobians, which helps recovering the true latent factors. The gap between ELBO and log-likelihood is therefore welcome, since it bears unanticipated benefits for nonlinear representation learning. In experiments on synthetic and image data, we show that VAEs uncover the true latent factors when the data generating process satisfies the IMA assumption.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge