Quantifying Sources of Uncertainty in Deep Learning-Based Image Reconstruction
Paper and Code
Nov 30, 2020

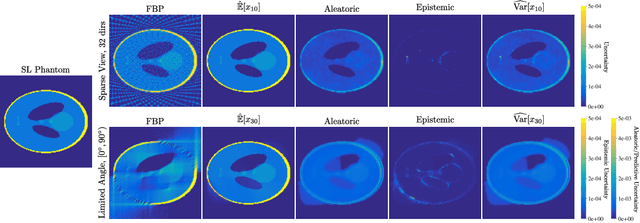

Image reconstruction methods based on deep neural networks have shown outstanding performance, equalling or exceeding the state-of-the-art results of conventional approaches, but often do not provide uncertainty information about the reconstruction. In this work we propose a scalable and efficient framework to simultaneously quantify aleatoric and epistemic uncertainties in learned iterative image reconstruction. We build on a Bayesian deep gradient descent method for quantifying epistemic uncertainty, and incorporate the heteroscedastic variance of the noise to account for the aleatoric uncertainty. We show that our method exhibits competitive performance against conventional benchmarks for computed tomography with both sparse view and limited angle data. The estimated uncertainty captures the variability in the reconstructions, caused by the restricted measurement model, and by missing information, due to the limited angle geometry.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge