A Probabilistic Deep Image Prior for Computational Tomography

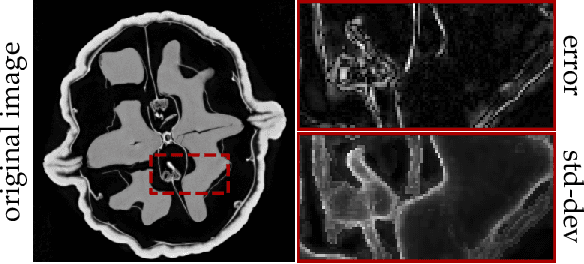
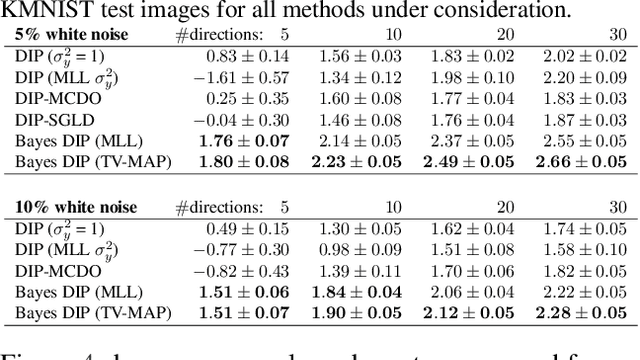
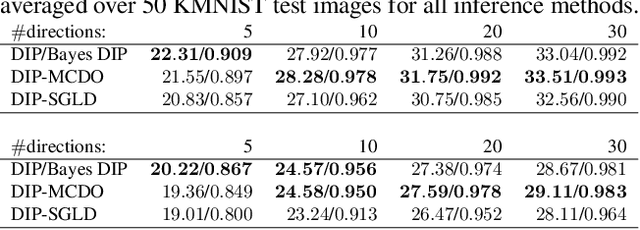
Existing deep-learning based tomographic image reconstruction methods do not provide accurate estimates of reconstruction uncertainty, hindering their real-world deployment. To address this limitation, we construct a Bayesian prior for tomographic reconstruction, which combines the classical total variation (TV) regulariser with the modern deep image prior (DIP). Specifically, we use a change of variables to connect our prior beliefs on the image TV semi-norm with the hyper-parameters of the DIP network. For the inference, we develop an approach based on the linearised Laplace method, which is scalable to high-dimensional settings. The resulting framework provides pixel-wise uncertainty estimates and a marginal likelihood objective for hyperparameter optimisation. We demonstrate the method on synthetic and real-measured high-resolution $\mu$CT data, and show that it provides superior calibration of uncertainty estimates relative to previous probabilistic formulations of the DIP.