James McInerney
Entropy After $\langle \texttt{/Think} \rangle$ for reasoning model early exiting
Sep 30, 2025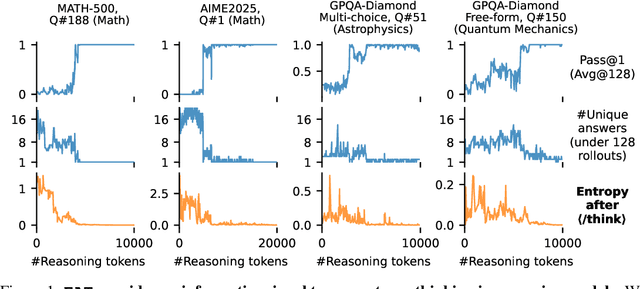

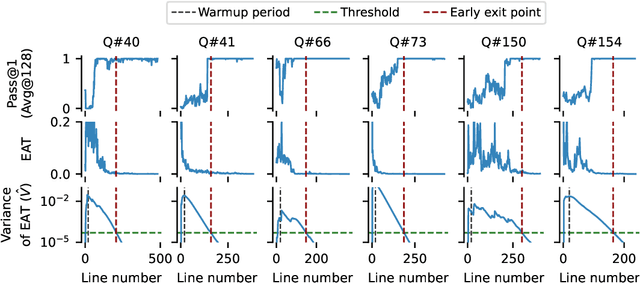
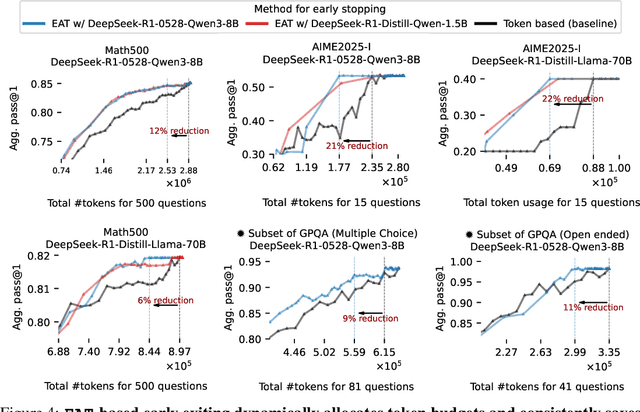
Abstract:Large reasoning models show improved performance with longer chains of thought. However, recent work has highlighted (qualitatively) their tendency to overthink, continuing to revise answers even after reaching the correct solution. We quantitatively confirm this inefficiency by tracking Pass@1 for answers averaged over a large number of rollouts and find that the model often begins to always produce the correct answer early in the reasoning, making extra reasoning a waste of tokens. To detect and prevent overthinking, we propose a simple and inexpensive novel signal -- Entropy After </Think> (EAT) -- for monitoring and deciding whether to exit reasoning early. By appending a stop thinking token (</think>) and monitoring the entropy of the following token as the model reasons, we obtain a trajectory that decreases and stabilizes when Pass@1 plateaus; thresholding its variance under an exponential moving average yields a practical stopping rule. Importantly, our approach enables adaptively allocating compute based on the EAT trajectory, allowing us to spend compute in a more efficient way compared with fixing the token budget for all questions. Empirically, on MATH500 and AIME2025, EAT reduces token usage by 13 - 21% without harming accuracy, and it remains effective in black box settings where logits from the reasoning model are not accessible, and EAT is computed with proxy models.
Adjusting Regression Models for Conditional Uncertainty Calibration
Sep 26, 2024Abstract:Conformal Prediction methods have finite-sample distribution-free marginal coverage guarantees. However, they generally do not offer conditional coverage guarantees, which can be important for high-stakes decisions. In this paper, we propose a novel algorithm to train a regression function to improve the conditional coverage after applying the split conformal prediction procedure. We establish an upper bound for the miscoverage gap between the conditional coverage and the nominal coverage rate and propose an end-to-end algorithm to control this upper bound. We demonstrate the efficacy of our method empirically on synthetic and real-world datasets.
Hessian-Free Laplace in Bayesian Deep Learning
Mar 15, 2024Abstract:The Laplace approximation (LA) of the Bayesian posterior is a Gaussian distribution centered at the maximum a posteriori estimate. Its appeal in Bayesian deep learning stems from the ability to quantify uncertainty post-hoc (i.e., after standard network parameter optimization), the ease of sampling from the approximate posterior, and the analytic form of model evidence. However, an important computational bottleneck of LA is the necessary step of calculating and inverting the Hessian matrix of the log posterior. The Hessian may be approximated in a variety of ways, with quality varying with a number of factors including the network, dataset, and inference task. In this paper, we propose an alternative framework that sidesteps Hessian calculation and inversion. The Hessian-free Laplace (HFL) approximation uses curvature of both the log posterior and network prediction to estimate its variance. Only two point estimates are needed: the standard maximum a posteriori parameter and the optimal parameter under a loss regularized by the network prediction. We show that, under standard assumptions of LA in Bayesian deep learning, HFL targets the same variance as LA, and can be efficiently amortized in a pre-trained network. Experiments demonstrate comparable performance to that of exact and approximate Hessians, with excellent coverage for in-between uncertainty.
Switching the Loss Reduces the Cost in Batch Reinforcement Learning
Mar 12, 2024
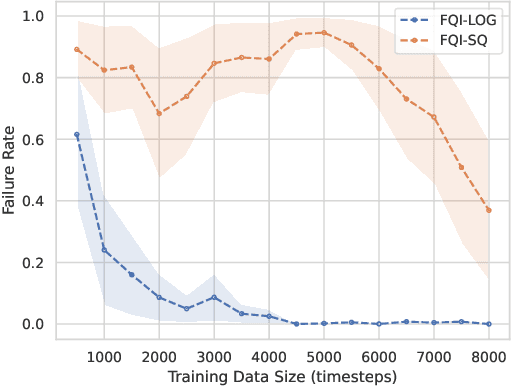
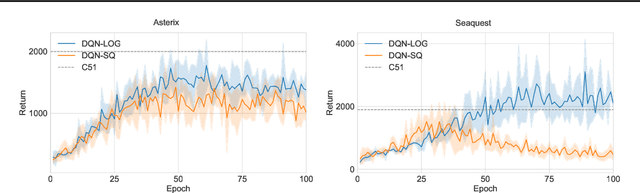
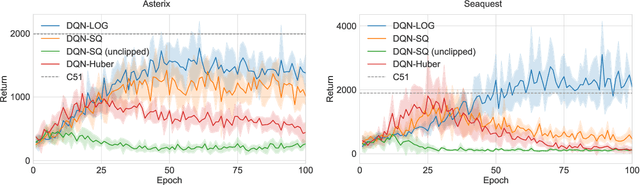
Abstract:We propose training fitted Q-iteration with log-loss (FQI-LOG) for batch reinforcement learning (RL). We show that the number of samples needed to learn a near-optimal policy with FQI-LOG scales with the accumulated cost of the optimal policy, which is zero in problems where acting optimally achieves the goal and incurs no cost. In doing so, we provide a general framework for proving $\textit{small-cost}$ bounds, i.e. bounds that scale with the optimal achievable cost, in batch RL. Moreover, we empirically verify that FQI-LOG uses fewer samples than FQI trained with squared loss on problems where the optimal policy reliably achieves the goal.
The Implicit Delta Method
Nov 11, 2022Abstract:Epistemic uncertainty quantification is a crucial part of drawing credible conclusions from predictive models, whether concerned about the prediction at a given point or any downstream evaluation that uses the model as input. When the predictive model is simple and its evaluation differentiable, this task is solved by the delta method, where we propagate the asymptotically-normal uncertainty in the predictive model through the evaluation to compute standard errors and Wald confidence intervals. However, this becomes difficult when the model and/or evaluation becomes more complex. Remedies include the bootstrap, but it can be computationally infeasible when training the model even once is costly. In this paper, we propose an alternative, the implicit delta method, which works by infinitesimally regularizing the training loss of the predictive model to automatically assess downstream uncertainty. We show that the change in the evaluation due to regularization is consistent for the asymptotic variance of the evaluation estimator, even when the infinitesimal change is approximated by a finite difference. This provides both a reliable quantification of uncertainty in terms of standard errors as well as permits the construction of calibrated confidence intervals. We discuss connections to other approaches to uncertainty quantification, both Bayesian and frequentist, and demonstrate our approach empirically.
Residual Overfit Method of Exploration
Oct 06, 2021Abstract:Exploration is a crucial aspect of bandit and reinforcement learning algorithms. The uncertainty quantification necessary for exploration often comes from either closed-form expressions based on simple models or resampling and posterior approximations that are computationally intensive. We propose instead an approximate exploration methodology based on fitting only two point estimates, one tuned and one overfit. The approach, which we term the residual overfit method of exploration (ROME), drives exploration towards actions where the overfit model exhibits the most overfitting compared to the tuned model. The intuition is that overfitting occurs the most at actions and contexts with insufficient data to form accurate predictions of the reward. We justify this intuition formally from both a frequentist and a Bayesian information theoretic perspective. The result is a method that generalizes to a wide variety of models and avoids the computational overhead of resampling or posterior approximations. We compare ROME against a set of established contextual bandit methods on three datasets and find it to be one of the best performing.
Counterfactual Evaluation of Slate Recommendations with Sequential Reward Interactions
Aug 24, 2020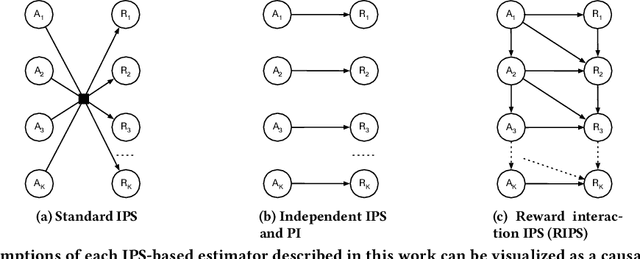
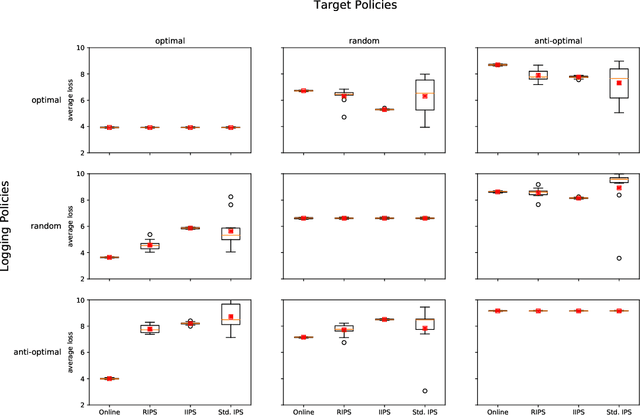
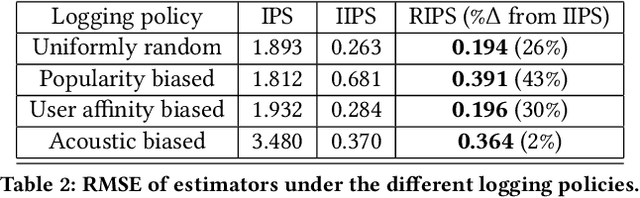
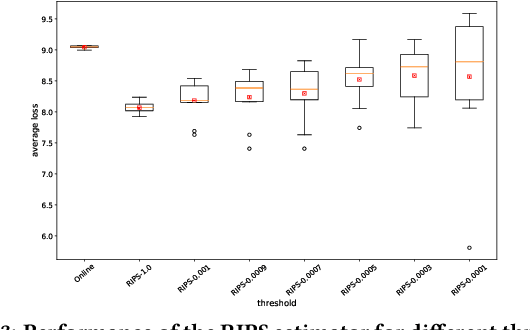
Abstract:Users of music streaming, video streaming, news recommendation, and e-commerce services often engage with content in a sequential manner. Providing and evaluating good sequences of recommendations is therefore a central problem for these services. Prior reweighting-based counterfactual evaluation methods either suffer from high variance or make strong independence assumptions about rewards. We propose a new counterfactual estimator that allows for sequential interactions in the rewards with lower variance in an asymptotically unbiased manner. Our method uses graphical assumptions about the causal relationships of the slate to reweight the rewards in the logging policy in a way that approximates the expected sum of rewards under the target policy. Extensive experiments in simulation and on a live recommender system show that our approach outperforms existing methods in terms of bias and data efficiency for the sequential track recommendations problem.
Variational Tempering
May 28, 2016



Abstract:Variational inference (VI) combined with data subsampling enables approximate posterior inference over large data sets, but suffers from poor local optima. We first formulate a deterministic annealing approach for the generic class of conditionally conjugate exponential family models. This approach uses a decreasing temperature parameter which deterministically deforms the objective during the course of the optimization. A well-known drawback to this annealing approach is the choice of the cooling schedule. We therefore introduce variational tempering, a variational algorithm that introduces a temperature latent variable to the model. In contrast to related work in the Markov chain Monte Carlo literature, this algorithm results in adaptive annealing schedules. Lastly, we develop local variational tempering, which assigns a latent temperature to each data point; this allows for dynamic annealing that varies across data. Compared to the traditional VI, all proposed approaches find improved predictive likelihoods on held-out data.
* published version, 8 pages, 4 figures
Modeling User Exposure in Recommendation
Feb 04, 2016



Abstract:Collaborative filtering analyzes user preferences for items (e.g., books, movies, restaurants, academic papers) by exploiting the similarity patterns across users. In implicit feedback settings, all the items, including the ones that a user did not consume, are taken into consideration. But this assumption does not accord with the common sense understanding that users have a limited scope and awareness of items. For example, a user might not have heard of a certain paper, or might live too far away from a restaurant to experience it. In the language of causal analysis, the assignment mechanism (i.e., the items that a user is exposed to) is a latent variable that may change for various user/item combinations. In this paper, we propose a new probabilistic approach that directly incorporates user exposure to items into collaborative filtering. The exposure is modeled as a latent variable and the model infers its value from data. In doing so, we recover one of the most successful state-of-the-art approaches as a special case of our model, and provide a plug-in method for conditioning exposure on various forms of exposure covariates (e.g., topics in text, venue locations). We show that our scalable inference algorithm outperforms existing benchmarks in four different domains both with and without exposure covariates.
Dynamic Poisson Factorization
Sep 15, 2015



Abstract:Models for recommender systems use latent factors to explain the preferences and behaviors of users with respect to a set of items (e.g., movies, books, academic papers). Typically, the latent factors are assumed to be static and, given these factors, the observed preferences and behaviors of users are assumed to be generated without order. These assumptions limit the explorative and predictive capabilities of such models, since users' interests and item popularity may evolve over time. To address this, we propose dPF, a dynamic matrix factorization model based on the recent Poisson factorization model for recommendations. dPF models the time evolving latent factors with a Kalman filter and the actions with Poisson distributions. We derive a scalable variational inference algorithm to infer the latent factors. Finally, we demonstrate dPF on 10 years of user click data from arXiv.org, one of the largest repository of scientific papers and a formidable source of information about the behavior of scientists. Empirically we show performance improvement over both static and, more recently proposed, dynamic recommendation models. We also provide a thorough exploration of the inferred posteriors over the latent variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge