Langevin Soft Actor-Critic: Efficient Exploration through Uncertainty-Driven Critic Learning

Existing actor-critic algorithms, which are popular for continuous control reinforcement learning (RL) tasks, suffer from poor sample efficiency due to lack of principled exploration mechanism within them. Motivated by the success of Thompson sampling for efficient exploration in RL, we propose a novel model-free RL algorithm, Langevin Soft Actor Critic (LSAC), which prioritizes enhancing critic learning through uncertainty estimation over policy optimization. LSAC employs three key innovations: approximate Thompson sampling through distributional Langevin Monte Carlo (LMC) based $Q$ updates, parallel tempering for exploring multiple modes of the posterior of the $Q$ function, and diffusion synthesized state-action samples regularized with $Q$ action gradients. Our extensive experiments demonstrate that LSAC outperforms or matches the performance of mainstream model-free RL algorithms for continuous control tasks. Notably, LSAC marks the first successful application of an LMC based Thompson sampling in continuous control tasks with continuous action spaces.

More Efficient Randomized Exploration for Reinforcement Learning via Approximate Sampling

Thompson sampling (TS) is one of the most popular exploration techniques in reinforcement learning (RL). However, most TS algorithms with theoretical guarantees are difficult to implement and not generalizable to Deep RL. While the emerging approximate sampling-based exploration schemes are promising, most existing algorithms are specific to linear Markov Decision Processes (MDP) with suboptimal regret bounds, or only use the most basic samplers such as Langevin Monte Carlo. In this work, we propose an algorithmic framework that incorporates different approximate sampling methods with the recently proposed Feel-Good Thompson Sampling (FGTS) approach (Zhang, 2022; Dann et al., 2021), which was previously known to be computationally intractable in general. When applied to linear MDPs, our regret analysis yields the best known dependency of regret on dimensionality, surpassing existing randomized algorithms. Additionally, we provide explicit sampling complexity for each employed sampler. Empirically, we show that in tasks where deep exploration is necessary, our proposed algorithms that combine FGTS and approximate sampling perform significantly better compared to other strong baselines. On several challenging games from the Atari 57 suite, our algorithms achieve performance that is either better than or on par with other strong baselines from the deep RL literature.

Offline Multitask Representation Learning for Reinforcement Learning

We study offline multitask representation learning in reinforcement learning (RL), where a learner is provided with an offline dataset from different tasks that share a common representation and is asked to learn the shared representation. We theoretically investigate offline multitask low-rank RL, and propose a new algorithm called MORL for offline multitask representation learning. Furthermore, we examine downstream RL in reward-free, offline and online scenarios, where a new task is introduced to the agent that shares the same representation as the upstream offline tasks. Our theoretical results demonstrate the benefits of using the learned representation from the upstream offline task instead of directly learning the representation of the low-rank model.

Provable and Practical: Efficient Exploration in Reinforcement Learning via Langevin Monte Carlo

We present a scalable and effective exploration strategy based on Thompson sampling for reinforcement learning (RL). One of the key shortcomings of existing Thompson sampling algorithms is the need to perform a Gaussian approximation of the posterior distribution, which is not a good surrogate in most practical settings. We instead directly sample the Q function from its posterior distribution, by using Langevin Monte Carlo, an efficient type of Markov Chain Monte Carlo (MCMC) method. Our method only needs to perform noisy gradient descent updates to learn the exact posterior distribution of the Q function, which makes our approach easy to deploy in deep RL. We provide a rigorous theoretical analysis for the proposed method and demonstrate that, in the linear Markov decision process (linear MDP) setting, it has a regret bound of $\tilde{O}(d^{3/2}H^{5/2}\sqrt{T})$, where $d$ is the dimension of the feature mapping, $H$ is the planning horizon, and $T$ is the total number of steps. We apply this approach to deep RL, by using Adam optimizer to perform gradient updates. Our approach achieves better or similar results compared with state-of-the-art deep RL algorithms on several challenging exploration tasks from the Atari57 suite.

Randomized Exploration for Reinforcement Learning with General Value Function Approximation

We propose a model-free reinforcement learning algorithm inspired by the popular randomized least squares value iteration (RLSVI) algorithm as well as the optimism principle. Unlike existing upper-confidence-bound (UCB) based approaches, which are often computationally intractable, our algorithm drives exploration by simply perturbing the training data with judiciously chosen i.i.d. scalar noises. To attain optimistic value function estimation without resorting to a UCB-style bonus, we introduce an optimistic reward sampling procedure. When the value functions can be represented by a function class $\mathcal{F}$, our algorithm achieves a worst-case regret bound of $\widetilde{O}(\mathrm{poly}(d_EH)\sqrt{T})$ where $T$ is the time elapsed, $H$ is the planning horizon and $d_E$ is the $\textit{eluder dimension}$ of $\mathcal{F}$. In the linear setting, our algorithm reduces to LSVI-PHE, a variant of RLSVI, that enjoys an $\widetilde{\mathcal{O}}(\sqrt{d^3H^3T})$ regret. We complement the theory with an empirical evaluation across known difficult exploration tasks.

Heuristics for Interpretable Knowledge Graph Contextualization

In this paper, we introduce the problem of knowledge graph contextualization that is, given a specific context, the problem of extracting the most relevant sub-graph of a given knowledge graph. The context in the case of this paper is defined to be the textual entailment problem, and more specifically an instance of that problem where the entailment relationship between two sentences P and H has to be predicted automatically. This prediction takes the form of a classification task, and we seek to provide that task with the most relevant external knowledge while eliminating as much noise as possible. We base our methodology on finding the shortest paths in the cost-customized external knowledge graph that connect P and H, and build a series of methods starting with manually curated search heuristics and culminating in automatically extracted heuristics to find such paths and build the most relevant sub-graph. We evaluate our approaches by measuring the accuracy of the classification on the textual entailment problem, and show that modulating the external knowledge that is used has an impact on performance.

TVAE: Triplet-Based Variational Autoencoder using Metric Learning

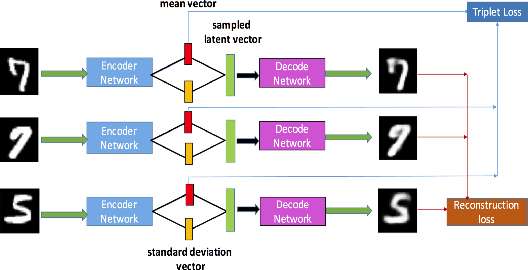
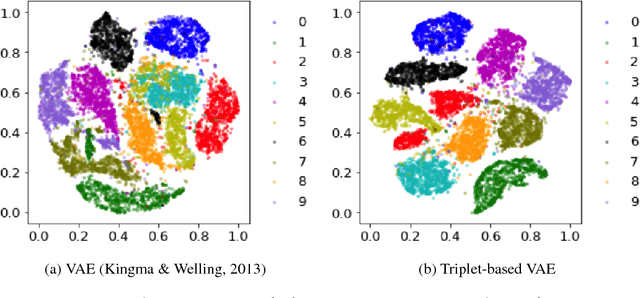
Deep metric learning has been demonstrated to be highly effective in learning semantic representation and encoding information that can be used to measure data similarity, by relying on the embedding learned from metric learning. At the same time, variational autoencoder (VAE) has widely been used to approximate inference and proved to have a good performance for directed probabilistic models. However, for traditional VAE, the data label or feature information are intractable. Similarly, traditional representation learning approaches fail to represent many salient aspects of the data. In this project, we propose a novel integrated framework to learn latent embedding in VAE by incorporating deep metric learning. The features are learned by optimizing a triplet loss on the mean vectors of VAE in conjunction with standard evidence lower bound (ELBO) of VAE. This approach, which we call Triplet based Variational Autoencoder (TVAE), allows us to capture more fine-grained information in the latent embedding. Our model is tested on MNIST data set and achieves a high triplet accuracy of 95.60% while the traditional VAE (Kingma & Welling, 2013) achieves triplet accuracy of 75.08%.