Optimistic Games for Combinatorial Bayesian Optimization with Application to Protein Design

Bayesian optimization (BO) is a powerful framework to optimize black-box expensive-to-evaluate functions via sequential interactions. In several important problems (e.g. drug discovery, circuit design, neural architecture search, etc.), though, such functions are defined over large $\textit{combinatorial and unstructured}$ spaces. This makes existing BO algorithms not feasible due to the intractable maximization of the acquisition function over these domains. To address this issue, we propose $\textbf{GameOpt}$, a novel game-theoretical approach to combinatorial BO. $\textbf{GameOpt}$ establishes a cooperative game between the different optimization variables, and selects points that are game $\textit{equilibria}$ of an upper confidence bound acquisition function. These are stable configurations from which no variable has an incentive to deviate$-$ analog to local optima in continuous domains. Crucially, this allows us to efficiently break down the complexity of the combinatorial domain into individual decision sets, making $\textbf{GameOpt}$ scalable to large combinatorial spaces. We demonstrate the application of $\textbf{GameOpt}$ to the challenging $\textit{protein design}$ problem and validate its performance on four real-world protein datasets. Each protein can take up to $20^{X}$ possible configurations, where $X$ is the length of a protein, making standard BO methods infeasible. Instead, our approach iteratively selects informative protein configurations and very quickly discovers highly active protein variants compared to other baselines.

Learning Controllers for Unstable Linear Quadratic Regulators from a Single Trajectory

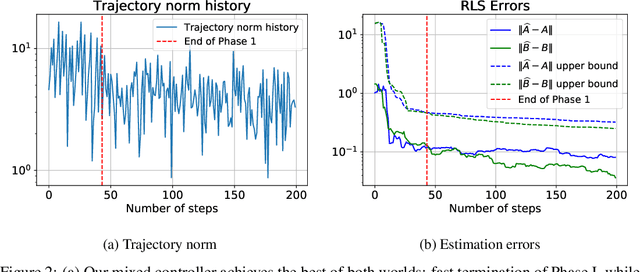
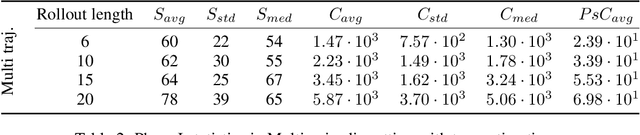
We present the first approach for learning -- from a single trajectory -- a linear quadratic regulator (LQR), even for unstable systems, without knowledge of the system dynamics and without requiring an initial stabilizing controller. Our central contribution is an efficient algorithm -- \emph{eXploration} -- that quickly identifies a stabilizing controller. Our approach utilizes robust System Level Synthesis (SLS), and we prove that it succeeds in a constant number of iterations. Our approach can be used to initialize existing algorithms that require a stabilizing controller as input. When used in this way, it yields a method for learning LQRs from a single trajectory and even for unstable systems, while suffering at most $\widetilde{\mathcal{O}}(\sqrt{T})$ regret.

Learning the Correction for Multi-Path Deviations in Time-of-Flight Cameras

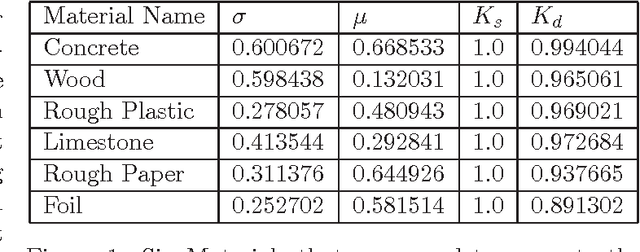
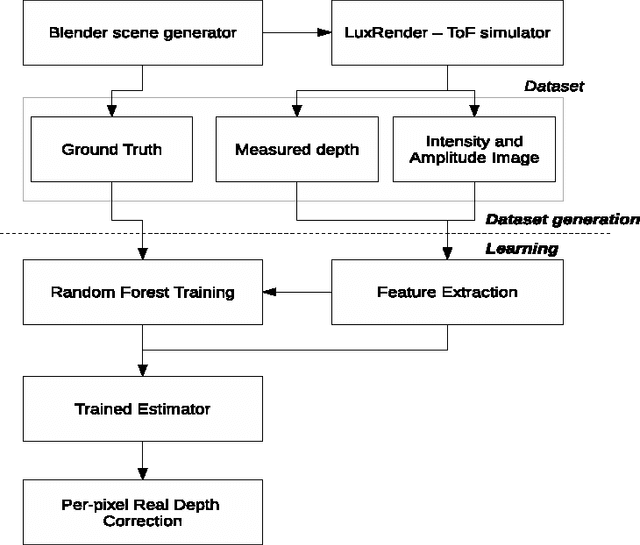
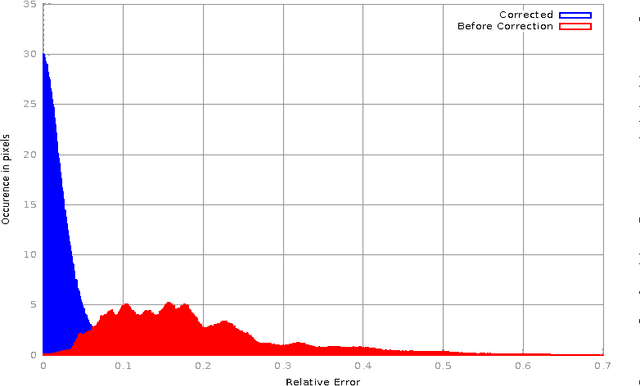
The Multipath effect in Time-of-Flight(ToF) cameras still remains to be a challenging problem that hinders further processing of 3D data information. Based on the evidence from previous literature, we explored the possibility of using machine learning techniques to correct this effect. Firstly, we created two new datasets of of ToF images rendered via ToF simulator of LuxRender. These two datasets contain corners in multiple orientations and with different material properties. We chose scenes with corners as multipath effects are most pronounced in corners. Secondly, we used this dataset to construct a learning model to predict real valued corrections to the ToF data using Random Forests. We found out that in our smaller dataset we were able to predict real valued correction and improve the quality of depth images significantly by removing multipath bias. With our algorithm, we improved relative per-pixel error from average value of 19% to 3%. Additionally, variance of the error was lowered by an order of magnitude.