Learning Controllers for Unstable Linear Quadratic Regulators from a Single Trajectory

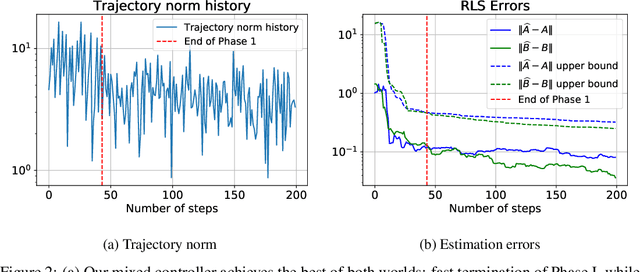
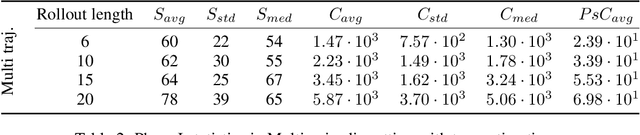
We present the first approach for learning -- from a single trajectory -- a linear quadratic regulator (LQR), even for unstable systems, without knowledge of the system dynamics and without requiring an initial stabilizing controller. Our central contribution is an efficient algorithm -- \emph{eXploration} -- that quickly identifies a stabilizing controller. Our approach utilizes robust System Level Synthesis (SLS), and we prove that it succeeds in a constant number of iterations. Our approach can be used to initialize existing algorithms that require a stabilizing controller as input. When used in this way, it yields a method for learning LQRs from a single trajectory and even for unstable systems, while suffering at most $\widetilde{\mathcal{O}}(\sqrt{T})$ regret.