Offline-to-Online Learning in Linear Bandits

We study online learning with an additional offline dataset in the stochastic linear bandit setting. Although this problem arises frequently in practice, the offline-to-online tradeoff remains poorly understood in structured environments. We propose a linear bandit algorithm that balances this tradeoff: it relies on offline data during early rounds, and increasingly favors exploration as the horizon grows. We establish regret bounds showing that our method is simultaneously competitive with both purely online and purely offline solutions. In particular, it achieves sublinear regret relative to the optimal action in the number of online interactions, while its regret relative to an offline reference decreases as the number of offline samples grows. Empirical results further demonstrate its effectiveness across various problem parameters.

Regret Minimization via Saddle Point Optimization

A long line of works characterizes the sample complexity of regret minimization in sequential decision-making by min-max programs. In the corresponding saddle-point game, the min-player optimizes the sampling distribution against an adversarial max-player that chooses confusing models leading to large regret. The most recent instantiation of this idea is the decision-estimation coefficient (DEC), which was shown to provide nearly tight lower and upper bounds on the worst-case expected regret in structured bandits and reinforcement learning. By re-parametrizing the offset DEC with the confidence radius and solving the corresponding min-max program, we derive an anytime variant of the Estimation-To-Decisions (E2D) algorithm. Importantly, the algorithm optimizes the exploration-exploitation trade-off online instead of via the analysis. Our formulation leads to a practical algorithm for finite model classes and linear feedback models. We further point out connections to the information ratio, decoupling coefficient and PAC-DEC, and numerically evaluate the performance of E2D on simple examples.

Combining Propositional Logic Based Decision Diagrams with Decision Making in Urban Systems

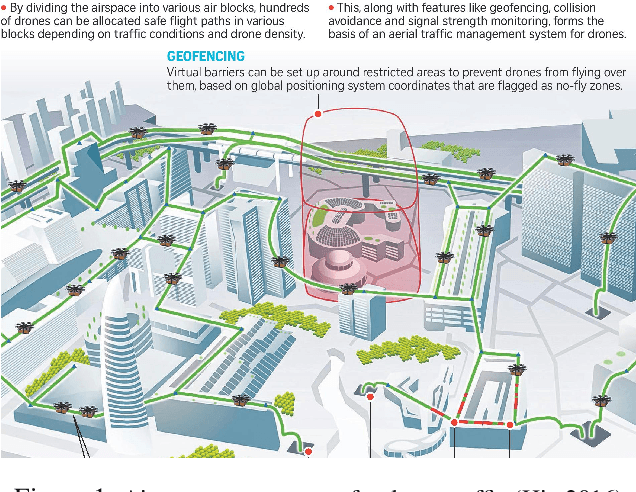
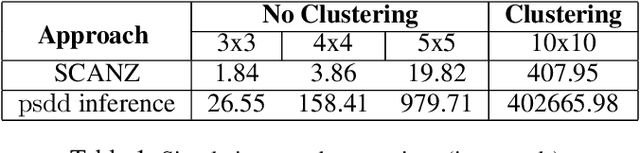
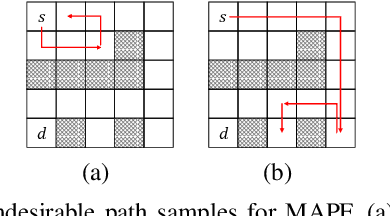
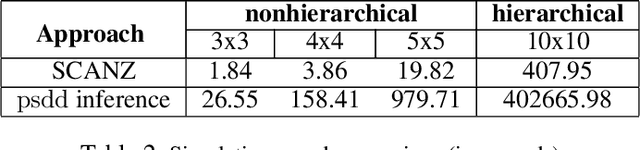
Solving multiagent problems can be an uphill task due to uncertainty in the environment, partial observability, and scalability of the problem at hand. Especially in an urban setting, there are more challenges since we also need to maintain safety for all users while minimizing congestion of the agents as well as their travel times. To this end, we tackle the problem of multiagent pathfinding under uncertainty and partial observability where the agents are tasked to move from their starting points to ending points while also satisfying some constraints, e.g., low congestion, and model it as a multiagent reinforcement learning problem. We compile the domain constraints using propositional logic and integrate them with the RL algorithms to enable fast simulation for RL.