FlowPG: Action-constrained Policy Gradient with Normalizing Flows

Action-constrained reinforcement learning (ACRL) is a popular approach for solving safety-critical and resource-allocation related decision making problems. A major challenge in ACRL is to ensure agent taking a valid action satisfying constraints in each RL step. Commonly used approach of using a projection layer on top of the policy network requires solving an optimization program which can result in longer training time, slow convergence, and zero gradient problem. To address this, first we use a normalizing flow model to learn an invertible, differentiable mapping between the feasible action space and the support of a simple distribution on a latent variable, such as Gaussian. Second, learning the flow model requires sampling from the feasible action space, which is also challenging. We develop multiple methods, based on Hamiltonian Monte-Carlo and probabilistic sentential decision diagrams for such action sampling for convex and non-convex constraints. Third, we integrate the learned normalizing flow with the DDPG algorithm. By design, a well-trained normalizing flow will transform policy output into a valid action without requiring an optimization solver. Empirically, our approach results in significantly fewer constraint violations (upto an order-of-magnitude for several instances) and is multiple times faster on a variety of continuous control tasks.

Combining Propositional Logic Based Decision Diagrams with Decision Making in Urban Systems

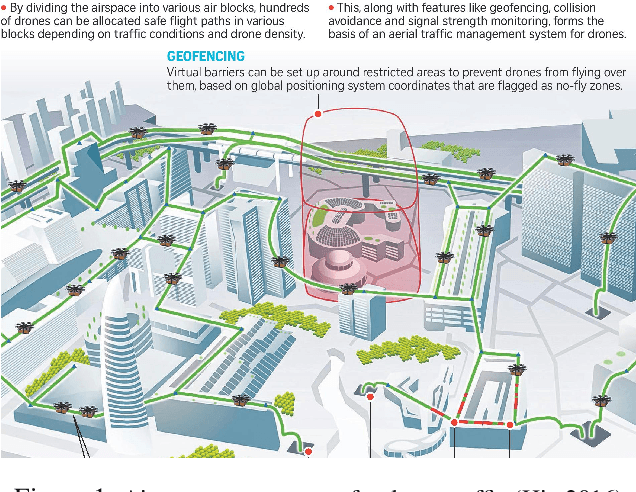
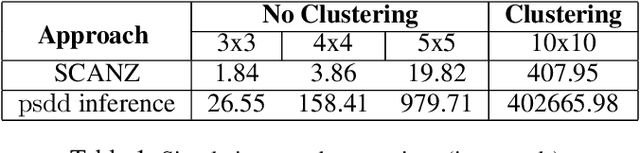
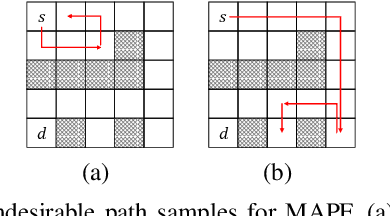
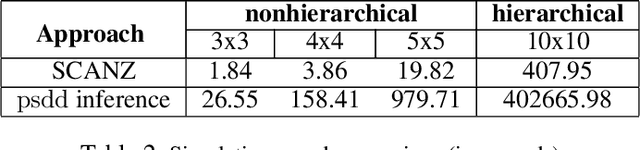
Solving multiagent problems can be an uphill task due to uncertainty in the environment, partial observability, and scalability of the problem at hand. Especially in an urban setting, there are more challenges since we also need to maintain safety for all users while minimizing congestion of the agents as well as their travel times. To this end, we tackle the problem of multiagent pathfinding under uncertainty and partial observability where the agents are tasked to move from their starting points to ending points while also satisfying some constraints, e.g., low congestion, and model it as a multiagent reinforcement learning problem. We compile the domain constraints using propositional logic and integrate them with the RL algorithms to enable fast simulation for RL.