Diffusion Active Learning: Towards Data-Driven Experimental Design in Computed Tomography

We introduce Diffusion Active Learning, a novel approach that combines generative diffusion modeling with data-driven sequential experimental design to adaptively acquire data for inverse problems. Although broadly applicable, we focus on scientific computed tomography (CT) for experimental validation, where structured prior datasets are available, and reducing data requirements directly translates to shorter measurement times and lower X-ray doses. We first pre-train an unconditional diffusion model on domain-specific CT reconstructions. The diffusion model acts as a learned prior that is data-dependent and captures the structure of the underlying data distribution, which is then used in two ways: It drives the active learning process and also improves the quality of the reconstructions. During the active learning loop, we employ a variant of diffusion posterior sampling to generate conditional data samples from the posterior distribution, ensuring consistency with the current measurements. Using these samples, we quantify the uncertainty in the current estimate to select the most informative next measurement. Our results show substantial reductions in data acquisition requirements, corresponding to lower X-ray doses, while simultaneously improving image reconstruction quality across multiple real-world tomography datasets.

Facial Tic Detection in Untrimmed Videos of Tourette Syndrome Patients

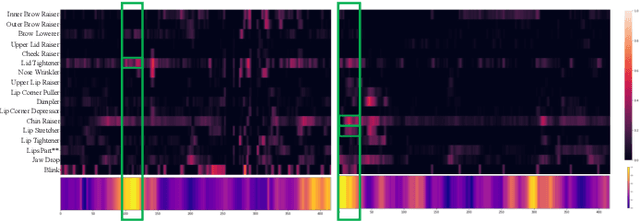
Tourette Syndrome (TS) is a behavior disorder that onsets in childhood and is characterized by the expression of involuntary movements and sounds commonly referred to as tics. Behavioral therapy is the first-line treatment for patients with TS, and it helps patients raise awareness about tic occurrence as well as develop tic inhibition strategies. However, the limited availability of therapists and the difficulties for in-home follow up work limits its effectiveness. An automatic tic detection system that is easy to deploy could alleviate the difficulties of home-therapy by providing feedback to the patients while exercising tic awareness. In this work, we propose a novel architecture (T-Net) for automatic tic detection and classification from untrimmed videos. T-Net combines temporal detection and segmentation and operates on features that are interpretable to a clinician. We compare T-Net to several state-of-the-art systems working on deep features extracted from the raw videos and T-Net achieves comparable performance in terms of average precision while relying on interpretable features needed in clinical practice.

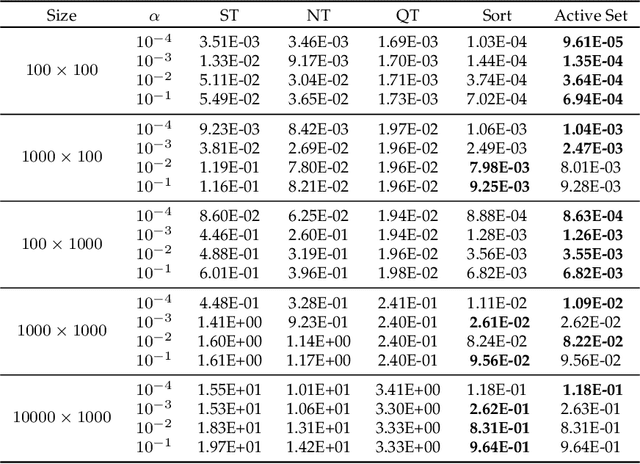
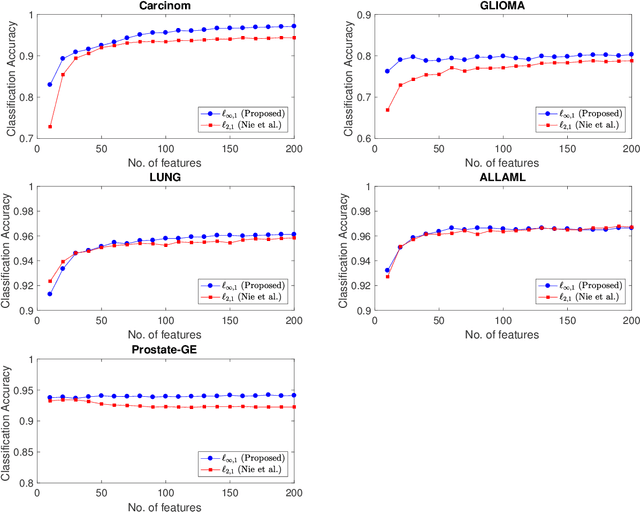
The fastest $\ell_{1,\infty}$ prox in the west

Proximal operators are of particular interest in optimization problems dealing with non-smooth objectives because in many practical cases they lead to optimization algorithms whose updates can be computed in closed form or very efficiently. A well-known example is the proximal operator of the vector $\ell_1$ norm, which is given by the soft-thresholding operator. In this paper we study the proximal operator of the mixed $\ell_{1,\infty}$ matrix norm and show that it can be computed in closed form by applying the well-known soft-thresholding operator to each column of the matrix. However, unlike the vector $\ell_1$ norm case where the threshold is constant, in the mixed $\ell_{1,\infty}$ norm case each column of the matrix might require a different threshold and all thresholds depend on the given matrix. We propose a general iterative algorithm for computing these thresholds, as well as two efficient implementations that further exploit easy to compute lower bounds for the mixed norm of the optimal solution. Experiments on large-scale synthetic and real data indicate that the proposed methods can be orders of magnitude faster than state-of-the-art methods.