Bias-Robust Bayesian Optimization via Dueling Bandits
Paper and Code
Jun 09, 2021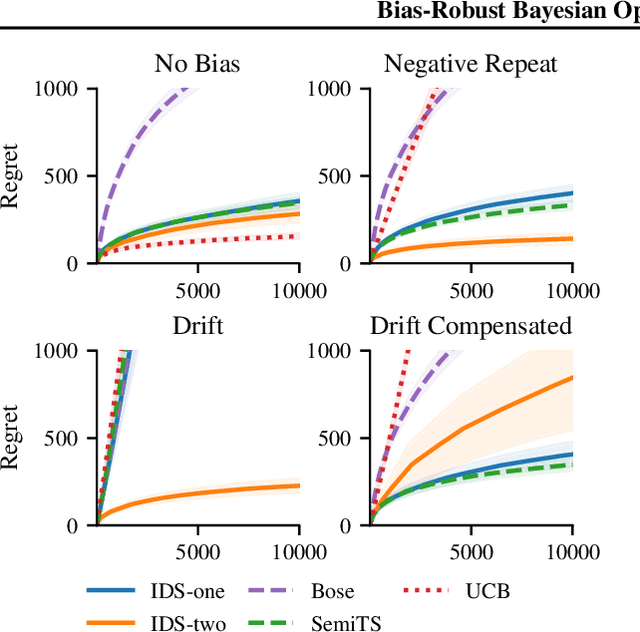
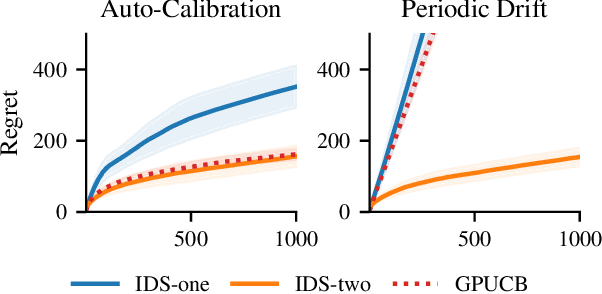
We consider Bayesian optimization in settings where observations can be adversarially biased, for example by an uncontrolled hidden confounder. Our first contribution is a reduction of the confounded setting to the dueling bandit model. Then we propose a novel approach for dueling bandits based on information-directed sampling (IDS). Thereby, we obtain the first efficient kernelized algorithm for dueling bandits that comes with cumulative regret guarantees. Our analysis further generalizes a previously proposed semi-parametric linear bandit model to non-linear reward functions, and uncovers interesting links to doubly-robust estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge