A Comparison of DeepSeek and Other LLMs

Recently, DeepSeek has been the focus of attention in and beyond the AI community. An interesting problem is how DeepSeek compares to other large language models (LLMs). There are many tasks an LLM can do, and in this paper, we use the task of predicting an outcome using a short text for comparison. We consider two settings, an authorship classification setting and a citation classification setting. In the first one, the goal is to determine whether a short text is written by human or AI. In the second one, the goal is to classify a citation to one of four types using the textual content. For each experiment, we compare DeepSeek with $4$ popular LLMs: Claude, Gemini, GPT, and Llama. We find that, in terms of classification accuracy, DeepSeek outperforms Gemini, GPT, and Llama in most cases, but underperforms Claude. We also find that DeepSeek is comparably slower than others but with a low cost to use, while Claude is much more expensive than all the others. Finally, we find that in terms of similarity, the output of DeepSeek is most similar to those of Gemini and Claude (and among all $5$ LLMs, Claude and Gemini have the most similar outputs). In this paper, we also present a fully-labeled dataset collected by ourselves, and propose a recipe where we can use the LLMs and a recent data set, MADStat, to generate new data sets. The datasets in our paper can be used as benchmarks for future study on LLMs.

Improved Algorithm and Bounds for Successive Projection

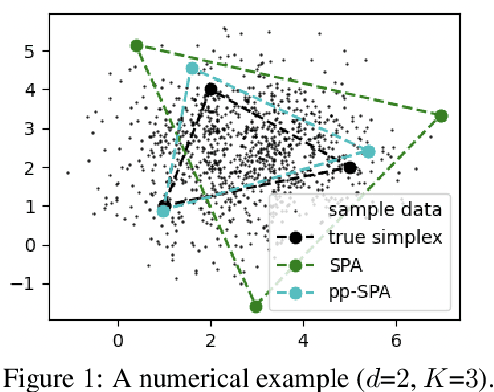
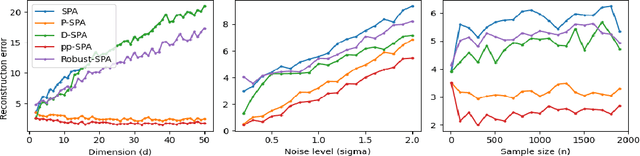
Given a $K$-vertex simplex in a $d$-dimensional space, suppose we measure $n$ points on the simplex with noise (hence, some of the observed points fall outside the simplex). Vertex hunting is the problem of estimating the $K$ vertices of the simplex. A popular vertex hunting algorithm is successive projection algorithm (SPA). However, SPA is observed to perform unsatisfactorily under strong noise or outliers. We propose pseudo-point SPA (pp-SPA). It uses a projection step and a denoise step to generate pseudo-points and feed them into SPA for vertex hunting. We derive error bounds for pp-SPA, leveraging on extreme value theory of (possibly) high-dimensional random vectors. The results suggest that pp-SPA has faster rates and better numerical performances than SPA. Our analysis includes an improved non-asymptotic bound for the original SPA, which is of independent interest.