Recent Advances in Text Analysis

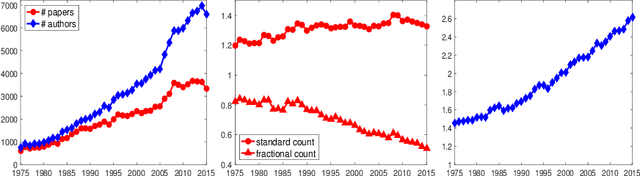
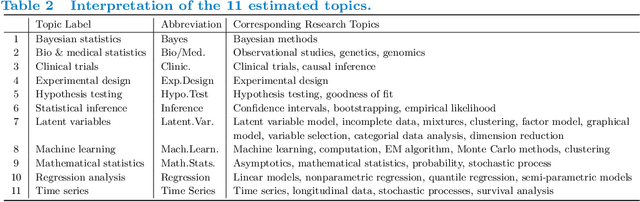
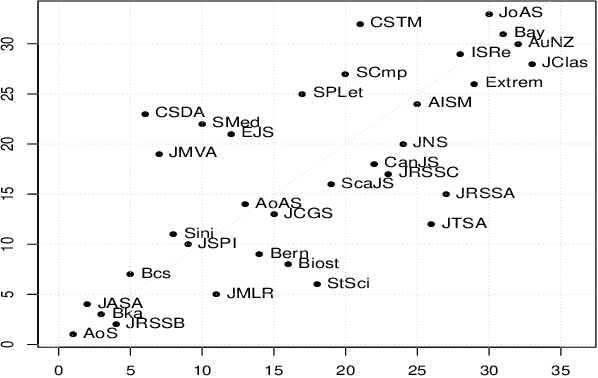
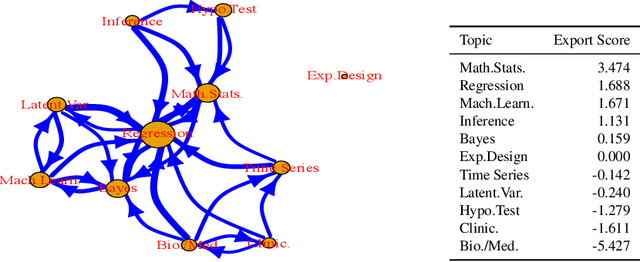
Text analysis is an interesting research area in data science and has various applications, such as in artificial intelligence, biomedical research, and engineering. We review popular methods for text analysis, ranging from topic modeling to the recent neural language models. In particular, we review Topic-SCORE, a statistical approach to topic modeling, and discuss how to use it to analyze MADStat - a dataset on statistical publications that we collected and cleaned. The application of Topic-SCORE and other methods on MADStat leads to interesting findings. For example, $11$ representative topics in statistics are identified. For each journal, the evolution of topic weights over time can be visualized, and these results are used to analyze the trends in statistical research. In particular, we propose a new statistical model for ranking the citation impacts of $11$ topics, and we also build a cross-topic citation graph to illustrate how research results on different topics spread to one another. The results on MADStat provide a data-driven picture of the statistical research in $1975$--$2015$, from a text analysis perspective.

The Performance of the MLE in the Bradley-Terry-Luce Model in $\ell_{\infty}$-Loss and under General Graph Topologies

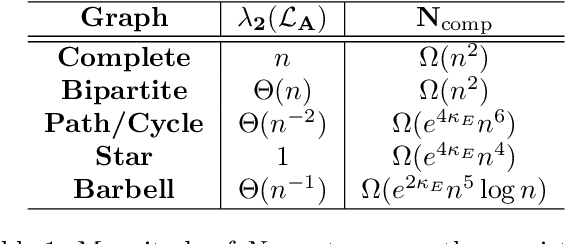
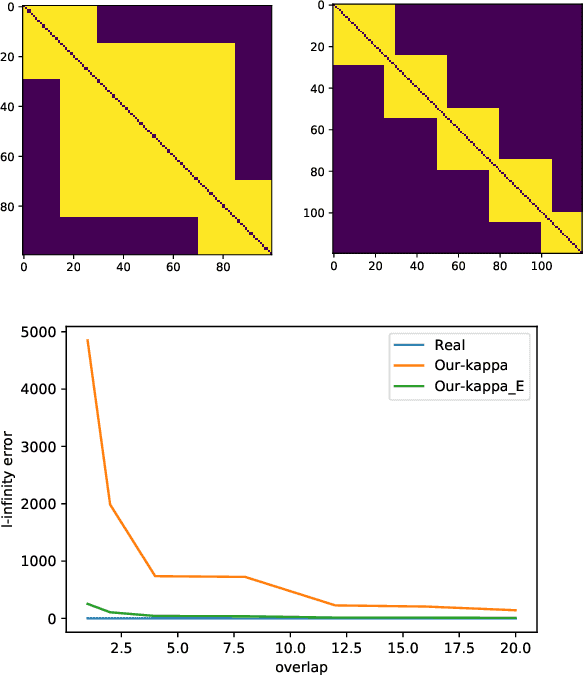
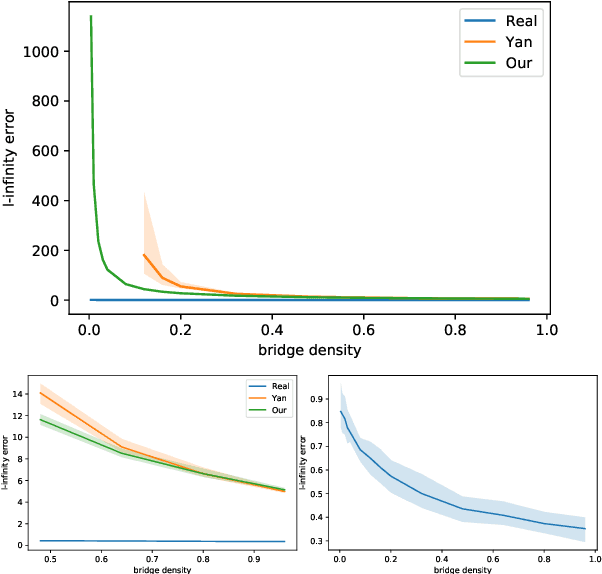
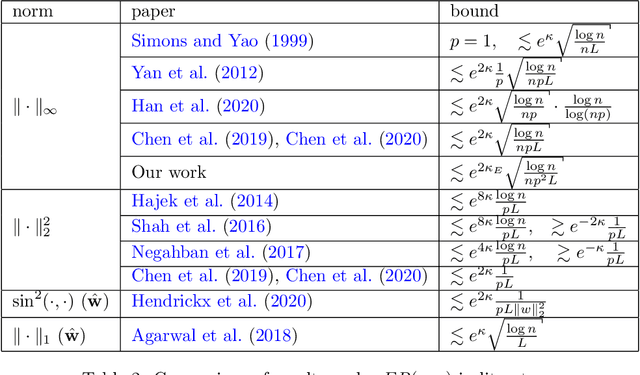
The Bradley-Terry-Luce (BTL) model is a popular statistical approach for estimating the global ranking of a collection of items of interest using pairwise comparisons. To ensure accurate ranking, it is essential to obtain precise estimates of the model parameters in the $\ell_{\infty}$-loss. The difficulty of this task depends crucially on the topology of the pairwise comparison graph over the given items. However, beyond very few well-studied cases, such as the complete and Erd\"os-R\'enyi comparison graphs, little is known about the performance of the maximum likelihood estimator (MLE) of the BTL model parameters in the $\ell_{\infty}$-loss under more general graph topologies. In this paper, we derive novel, general upper bounds on the $\ell_{\infty}$ estimation error of the BTL MLE that depend explicitly on the algebraic connectivity of the comparison graph, the maximal performance gap across items and the sample complexity. We demonstrate that the derived bounds perform well and in some cases are sharper compared to known results obtained using different loss functions and more restricted assumptions and graph topologies. We further provide minimax lower bounds under $\ell_{\infty}$-error that nearly match the upper bounds over a class of sufficiently regular graph topologies. Finally, we study the implications of our bounds for efficient tournament design. We illustrate and discuss our findings through various examples and simulations.

Nonparametric Estimation in the Dynamic Bradley-Terry Model

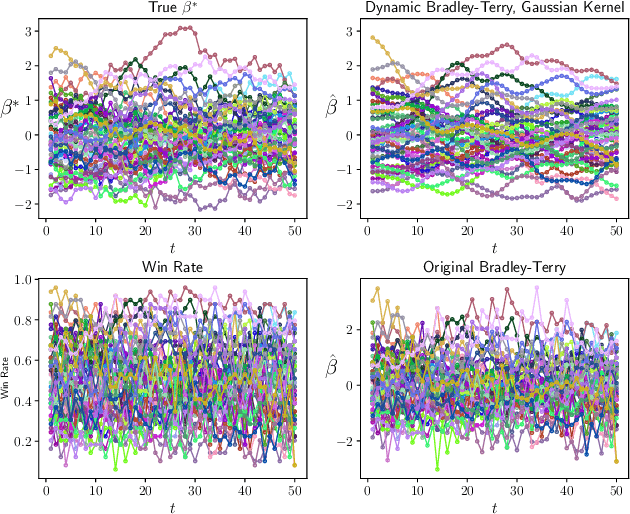
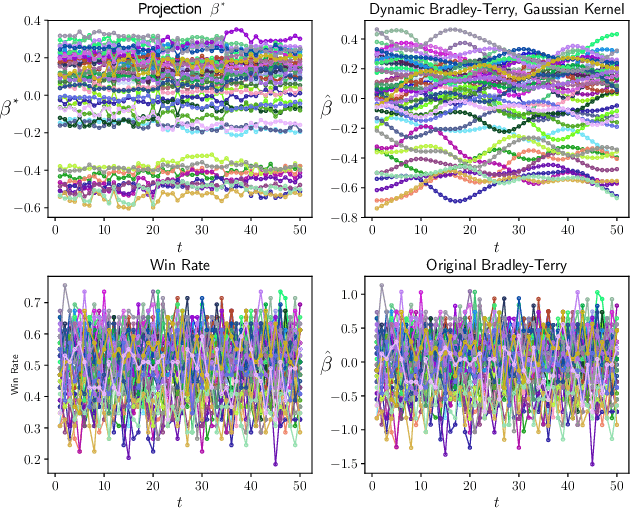
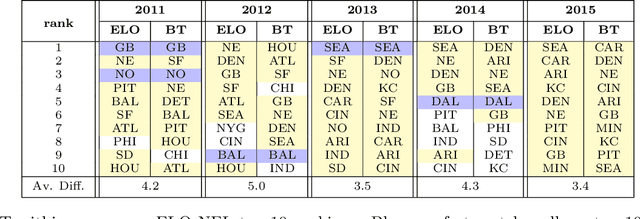
We propose a time-varying generalization of the Bradley-Terry model that allows for nonparametric modeling of dynamic global rankings of distinct teams. We develop a novel estimator that relies on kernel smoothing to pre-process the pairwise comparisons over time and is applicable in sparse settings where the Bradley-Terry may not be fit. We obtain necessary and sufficient conditions for the existence and uniqueness of our estimator. We also derive time-varying oracle bounds for both the estimation error and the excess risk in the model-agnostic setting where the Bradley-Terry model is not necessarily the true data generating process. We thoroughly test the practical effectiveness of our model using both simulated and real world data and suggest an efficient data-driven approach for bandwidth tuning.