The Performance of the MLE in the Bradley-Terry-Luce Model in $\ell_{\infty}$-Loss and under General Graph Topologies

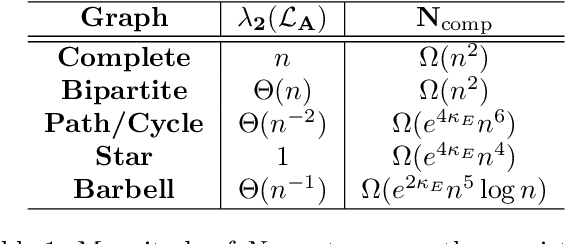
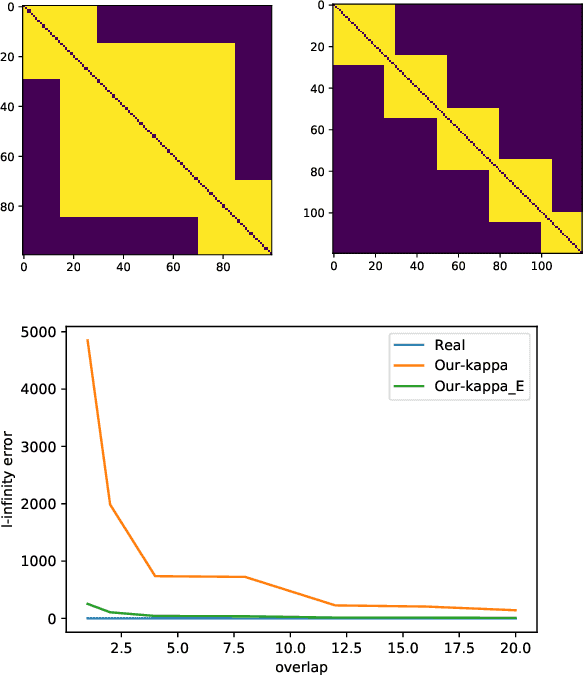
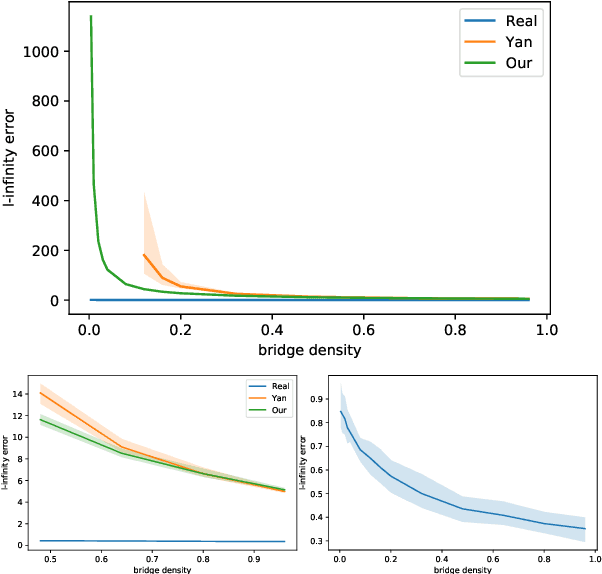
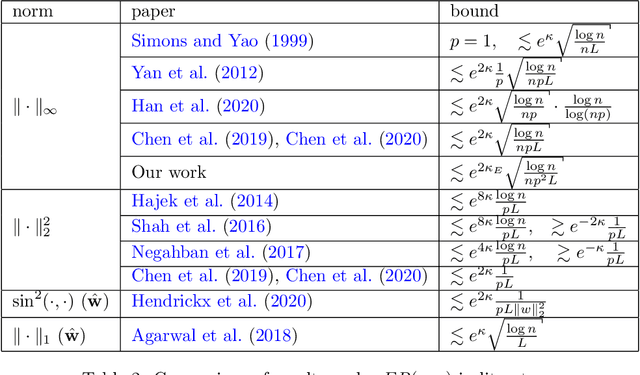
The Bradley-Terry-Luce (BTL) model is a popular statistical approach for estimating the global ranking of a collection of items of interest using pairwise comparisons. To ensure accurate ranking, it is essential to obtain precise estimates of the model parameters in the $\ell_{\infty}$-loss. The difficulty of this task depends crucially on the topology of the pairwise comparison graph over the given items. However, beyond very few well-studied cases, such as the complete and Erd\"os-R\'enyi comparison graphs, little is known about the performance of the maximum likelihood estimator (MLE) of the BTL model parameters in the $\ell_{\infty}$-loss under more general graph topologies. In this paper, we derive novel, general upper bounds on the $\ell_{\infty}$ estimation error of the BTL MLE that depend explicitly on the algebraic connectivity of the comparison graph, the maximal performance gap across items and the sample complexity. We demonstrate that the derived bounds perform well and in some cases are sharper compared to known results obtained using different loss functions and more restricted assumptions and graph topologies. We further provide minimax lower bounds under $\ell_{\infty}$-error that nearly match the upper bounds over a class of sufficiently regular graph topologies. Finally, we study the implications of our bounds for efficient tournament design. We illustrate and discuss our findings through various examples and simulations.