Revisiting Le Cam's Equation: Exact Minimax Rates over Convex Density Classes

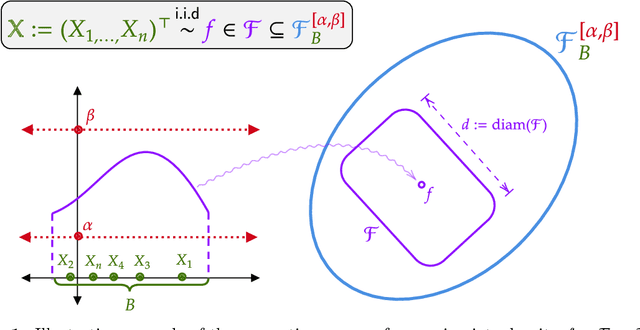
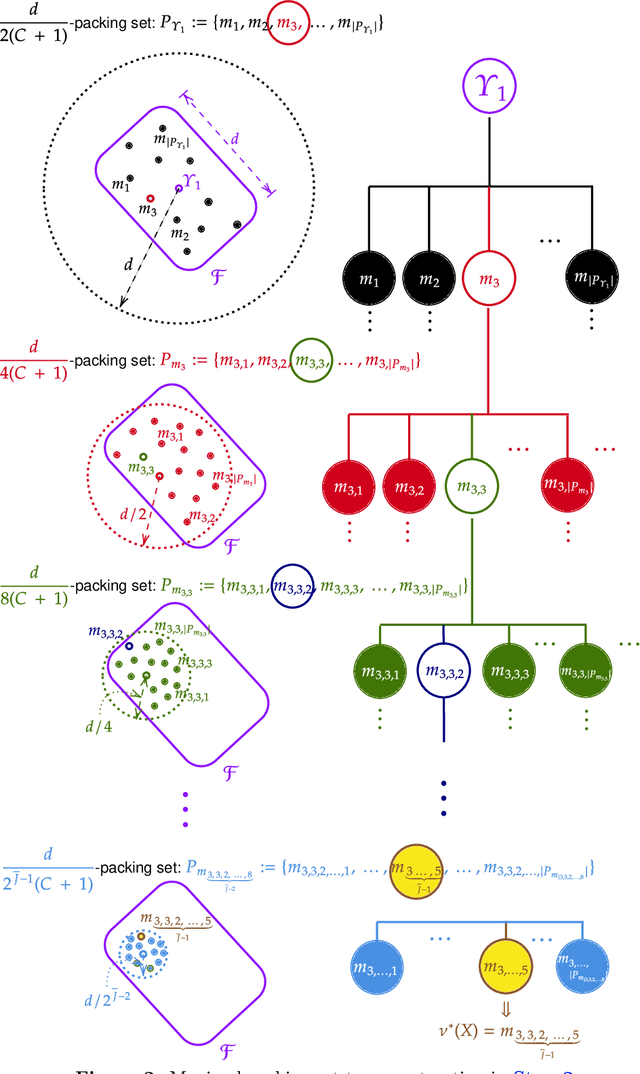
We study the classical problem of deriving minimax rates for density estimation over convex density classes. Building on the pioneering work of Le Cam (1973), Birge (1983, 1986), Wong and Shen (1995), Yang and Barron (1999), we determine the exact (up to constants) minimax rate over any convex density class. This work thus extends these known results by demonstrating that the local metric entropy of the density class always captures the minimax optimal rates under such settings. Our bounds provide a unifying perspective across both parametric and nonparametric convex density classes, under weaker assumptions on the richness of the density class than previously considered. Our proposed `multistage sieve' MLE applies to any such convex density class. We apply our risk bounds to rederive known minimax rates including bounded total variation, and Holder density classes. We further illustrate the utility of the result by deriving upper bounds for less studied classes, e.g., convex mixture of densities.

Adversarial Sign-Corrupted Isotonic Regression

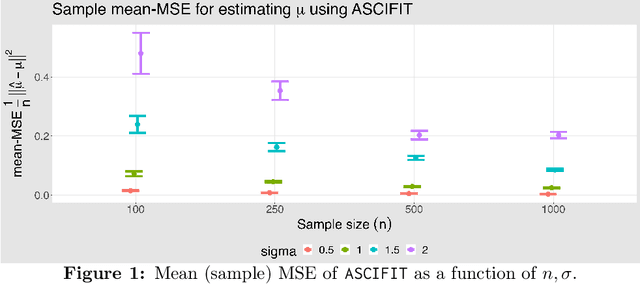
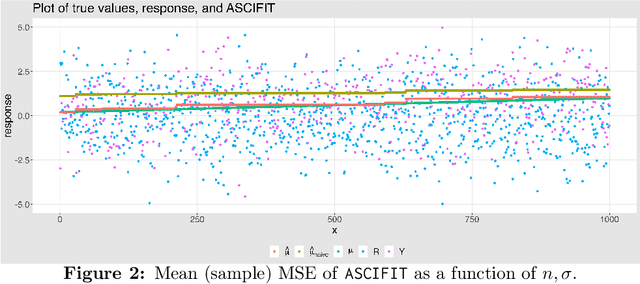
Classical univariate isotonic regression involves nonparametric estimation under a monotonicity constraint of the true signal. We consider a variation of this generating process, which we term adversarial sign-corrupted isotonic (\texttt{ASCI}) regression. Under this \texttt{ASCI} setting, the adversary has full access to the true isotonic responses, and is free to sign-corrupt them. Estimating the true monotonic signal given these sign-corrupted responses is a highly challenging task. Notably, the sign-corruptions are designed to violate monotonicity, and possibly induce heavy dependence between the corrupted response terms. In this sense, \texttt{ASCI} regression may be viewed as an adversarial stress test for isotonic regression. Our motivation is driven by understanding whether efficient robust estimation of the monotone signal is feasible under this adversarial setting. We develop \texttt{ASCIFIT}, a three-step estimation procedure under the \texttt{ASCI} setting. The \texttt{ASCIFIT} procedure is conceptually simple, easy to implement with existing software, and consists of applying the \texttt{PAVA} with crucial pre- and post-processing corrections. We formalize this procedure, and demonstrate its theoretical guarantees in the form of sharp high probability upper bounds and minimax lower bounds. We illustrate our findings with detailed simulations.

The Performance of the MLE in the Bradley-Terry-Luce Model in $\ell_{\infty}$-Loss and under General Graph Topologies

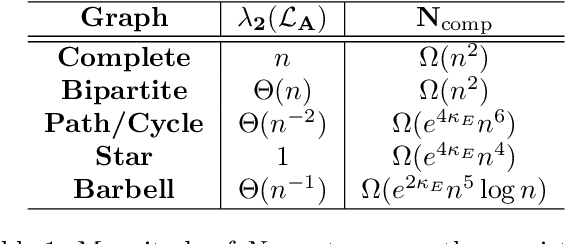
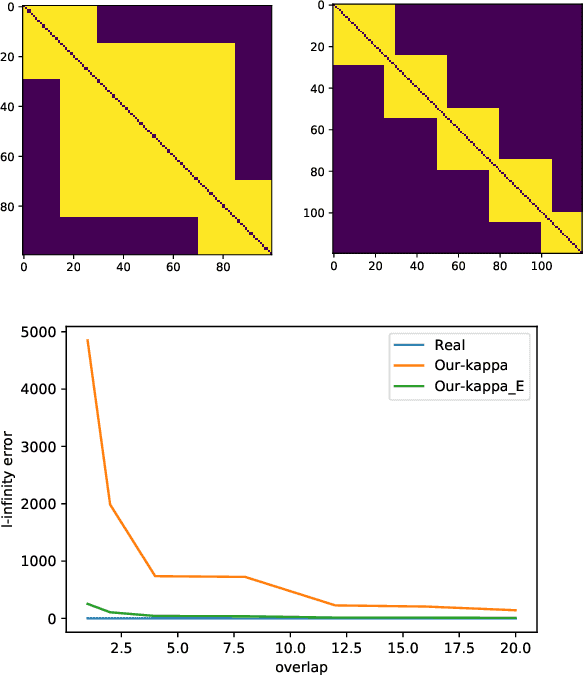
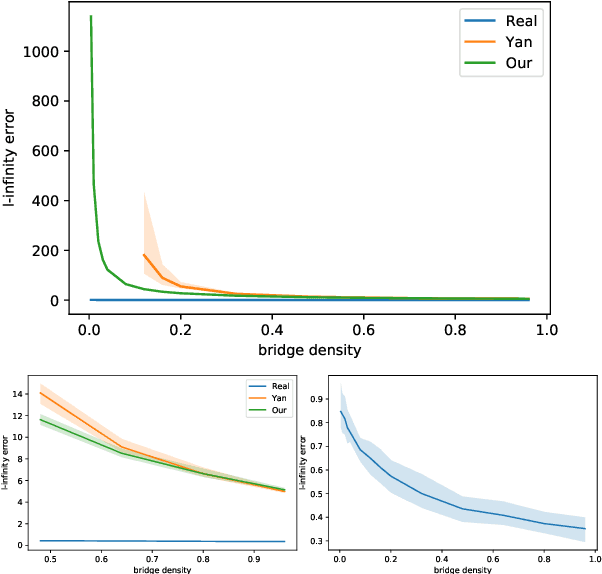
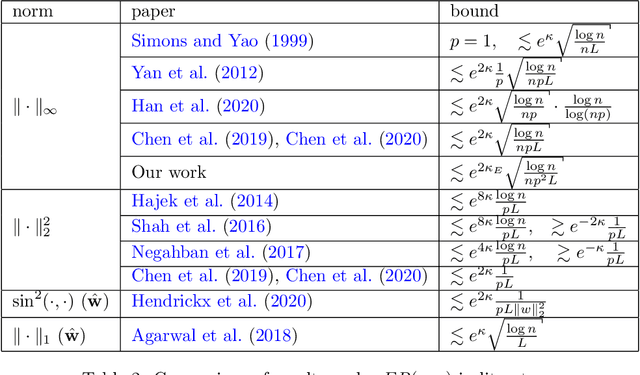
The Bradley-Terry-Luce (BTL) model is a popular statistical approach for estimating the global ranking of a collection of items of interest using pairwise comparisons. To ensure accurate ranking, it is essential to obtain precise estimates of the model parameters in the $\ell_{\infty}$-loss. The difficulty of this task depends crucially on the topology of the pairwise comparison graph over the given items. However, beyond very few well-studied cases, such as the complete and Erd\"os-R\'enyi comparison graphs, little is known about the performance of the maximum likelihood estimator (MLE) of the BTL model parameters in the $\ell_{\infty}$-loss under more general graph topologies. In this paper, we derive novel, general upper bounds on the $\ell_{\infty}$ estimation error of the BTL MLE that depend explicitly on the algebraic connectivity of the comparison graph, the maximal performance gap across items and the sample complexity. We demonstrate that the derived bounds perform well and in some cases are sharper compared to known results obtained using different loss functions and more restricted assumptions and graph topologies. We further provide minimax lower bounds under $\ell_{\infty}$-error that nearly match the upper bounds over a class of sufficiently regular graph topologies. Finally, we study the implications of our bounds for efficient tournament design. We illustrate and discuss our findings through various examples and simulations.

Nonparametric Estimation in the Dynamic Bradley-Terry Model

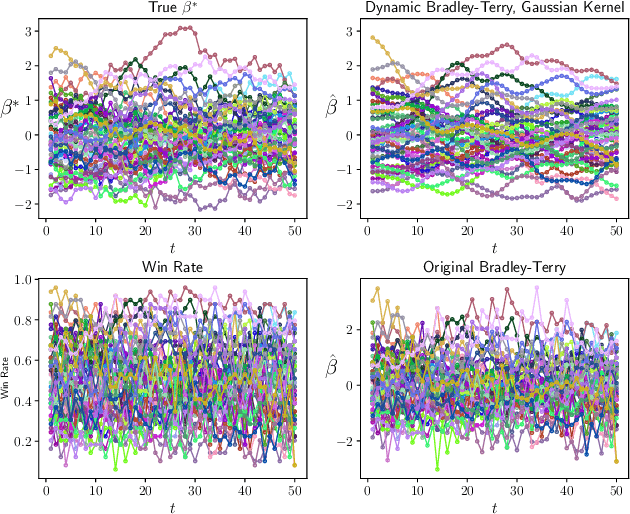
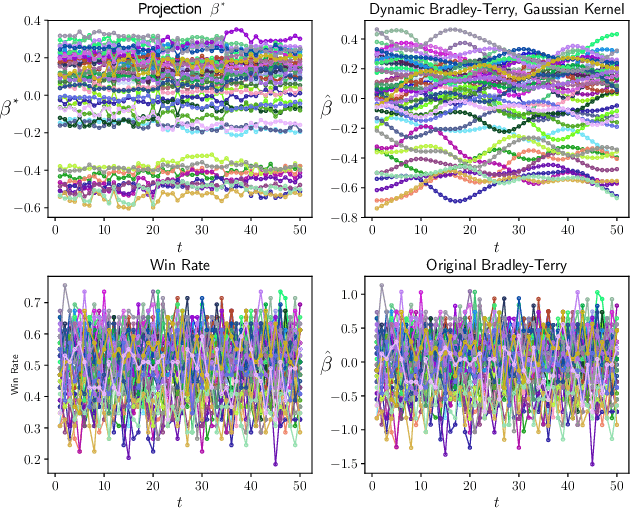
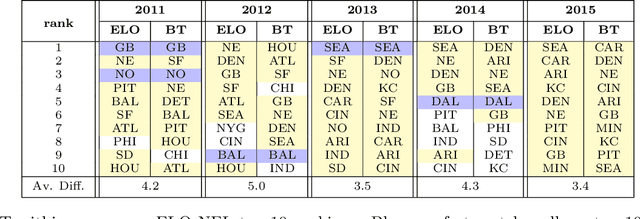
We propose a time-varying generalization of the Bradley-Terry model that allows for nonparametric modeling of dynamic global rankings of distinct teams. We develop a novel estimator that relies on kernel smoothing to pre-process the pairwise comparisons over time and is applicable in sparse settings where the Bradley-Terry may not be fit. We obtain necessary and sufficient conditions for the existence and uniqueness of our estimator. We also derive time-varying oracle bounds for both the estimation error and the excess risk in the model-agnostic setting where the Bradley-Terry model is not necessarily the true data generating process. We thoroughly test the practical effectiveness of our model using both simulated and real world data and suggest an efficient data-driven approach for bandwidth tuning.