Adversarial Sign-Corrupted Isotonic Regression
Paper and Code
Jul 14, 2022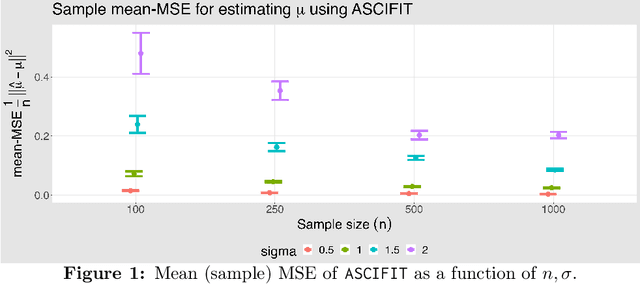
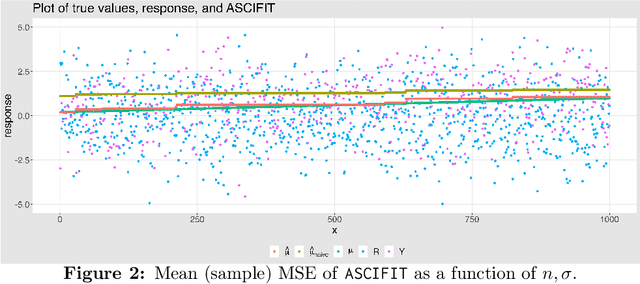
Classical univariate isotonic regression involves nonparametric estimation under a monotonicity constraint of the true signal. We consider a variation of this generating process, which we term adversarial sign-corrupted isotonic (\texttt{ASCI}) regression. Under this \texttt{ASCI} setting, the adversary has full access to the true isotonic responses, and is free to sign-corrupt them. Estimating the true monotonic signal given these sign-corrupted responses is a highly challenging task. Notably, the sign-corruptions are designed to violate monotonicity, and possibly induce heavy dependence between the corrupted response terms. In this sense, \texttt{ASCI} regression may be viewed as an adversarial stress test for isotonic regression. Our motivation is driven by understanding whether efficient robust estimation of the monotone signal is feasible under this adversarial setting. We develop \texttt{ASCIFIT}, a three-step estimation procedure under the \texttt{ASCI} setting. The \texttt{ASCIFIT} procedure is conceptually simple, easy to implement with existing software, and consists of applying the \texttt{PAVA} with crucial pre- and post-processing corrections. We formalize this procedure, and demonstrate its theoretical guarantees in the form of sharp high probability upper bounds and minimax lower bounds. We illustrate our findings with detailed simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge