Revisiting Le Cam's Equation: Exact Minimax Rates over Convex Density Classes
Paper and Code
Oct 20, 2022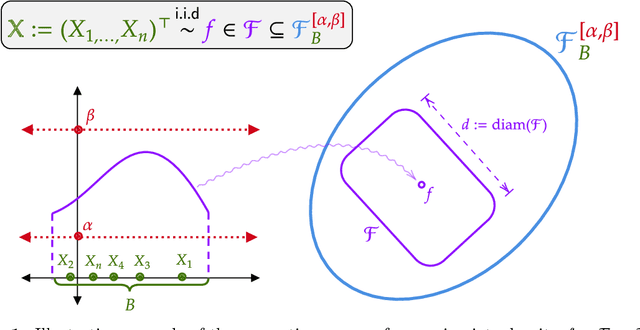
We study the classical problem of deriving minimax rates for density estimation over convex density classes. Building on the pioneering work of Le Cam (1973), Birge (1983, 1986), Wong and Shen (1995), Yang and Barron (1999), we determine the exact (up to constants) minimax rate over any convex density class. This work thus extends these known results by demonstrating that the local metric entropy of the density class always captures the minimax optimal rates under such settings. Our bounds provide a unifying perspective across both parametric and nonparametric convex density classes, under weaker assumptions on the richness of the density class than previously considered. Our proposed `multistage sieve' MLE applies to any such convex density class. We apply our risk bounds to rederive known minimax rates including bounded total variation, and Holder density classes. We further illustrate the utility of the result by deriving upper bounds for less studied classes, e.g., convex mixture of densities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge