Quantum Discriminator for Binary Classification
Paper and Code
Sep 02, 2020

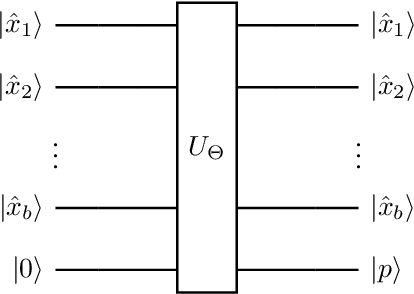

Quantum computers operate in the high-dimensional tensor product spaces and are known to outperform classical computers on many problems. They are poised to accelerate machine learning tasks in the future. In this work, we operate in the quantum machine learning (QML) regime where a QML model is trained using a quantum-classical hybrid algorithm and inferencing is performed using a quantum algorithm. We leverage the traditional two-step machine learning workflow, where features are extracted from the data in the first step and a discriminator acting on the extracted features is used to classify the data in the second step. Assuming that the binary features have been extracted from the data, we propose a quantum discriminator for binary classification. The quantum discriminator takes as input the binary features of a data point and a prediction qubit in the zero state, and outputs the correct class of the data point. The quantum discriminator is defined by a parameterized unitary matrix $U_\Theta$ containing $\mathcal{O}(N)$ parameters, where $N$ is the number of data points in the training data set. Furthermore, we show that the quantum discriminator can be trained in $\mathcal{O}(N \log N)$ time using $\mathcal{O}(N \log N)$ classical bits and $\mathcal{O}(\log N)$ qubits. We also show that inferencing for the quantum discriminator can be done in $\mathcal{O}(N)$ time using $\mathcal{O}(\log N)$ qubits. Finally, we use the quantum discriminator to classify the XOR problem on the IBM Q universal quantum computer with $100\%$ accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge