NeuroCoreX: An Open-Source FPGA-Based Spiking Neural Network Emulator with On-Chip Learning

Spiking Neural Networks (SNNs) are computational models inspired by the structure and dynamics of biological neuronal networks. Their event-driven nature enables them to achieve high energy efficiency, particularly when deployed on neuromorphic hardware platforms. Unlike conventional Artificial Neural Networks (ANNs), which primarily rely on layered architectures, SNNs naturally support a wide range of connectivity patterns, from traditional layered structures to small-world graphs characterized by locally dense and globally sparse connections. In this work, we introduce NeuroCoreX, an FPGA-based emulator designed for the flexible co-design and testing of SNNs. NeuroCoreX supports all-to-all connectivity, providing the capability to implement diverse network topologies without architectural restrictions. It features a biologically motivated local learning mechanism based on Spike-Timing-Dependent Plasticity (STDP). The neuron model implemented within NeuroCoreX is the Leaky Integrate-and-Fire (LIF) model, with current-based synapses facilitating spike integration and transmission . A Universal Asynchronous Receiver-Transmitter (UART) interface is provided for programming and configuring the network parameters, including neuron, synapse, and learning rule settings. Users interact with the emulator through a simple Python-based interface, streamlining SNN deployment from model design to hardware execution. NeuroCoreX is released as an open-source framework, aiming to accelerate research and development in energy-efficient, biologically inspired computing.

SuperNeuro: A Fast and Scalable Simulator for Neuromorphic Computing

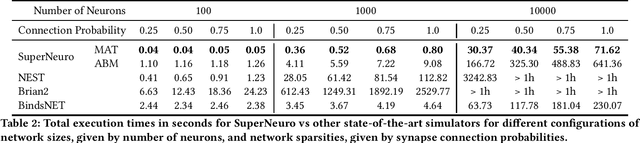
In many neuromorphic workflows, simulators play a vital role for important tasks such as training spiking neural networks (SNNs), running neuroscience simulations, and designing, implementing and testing neuromorphic algorithms. Currently available simulators are catered to either neuroscience workflows (such as NEST and Brian2) or deep learning workflows (such as BindsNET). While the neuroscience-based simulators are slow and not very scalable, the deep learning-based simulators do not support certain functionalities such as synaptic delay that are typical of neuromorphic workloads. In this paper, we address this gap in the literature and present SuperNeuro, which is a fast and scalable simulator for neuromorphic computing, capable of both homogeneous and heterogeneous simulations as well as GPU acceleration. We also present preliminary results comparing SuperNeuro to widely used neuromorphic simulators such as NEST, Brian2 and BindsNET in terms of computation times. We demonstrate that SuperNeuro can be approximately 10--300 times faster than some of the other simulators for small sparse networks. On large sparse and large dense networks, SuperNeuro can be approximately 2.2 and 3.4 times faster than the other simulators respectively.

Encoding Integers and Rationals on Neuromorphic Computers using Virtual Neuron

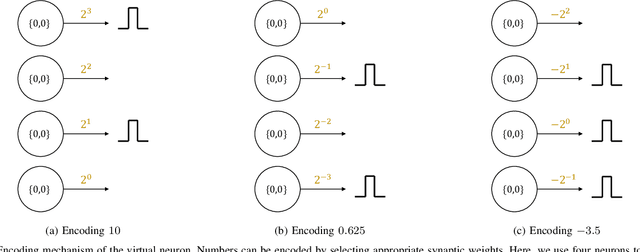
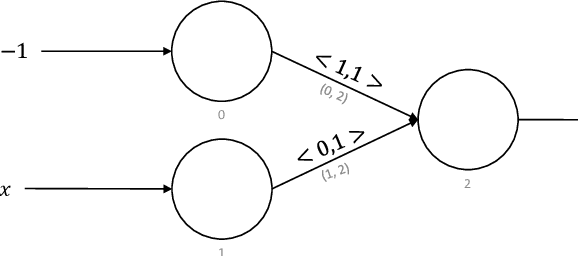
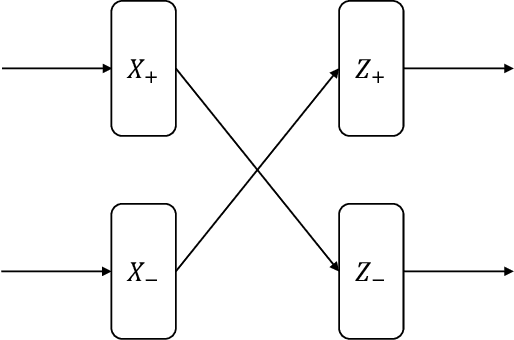
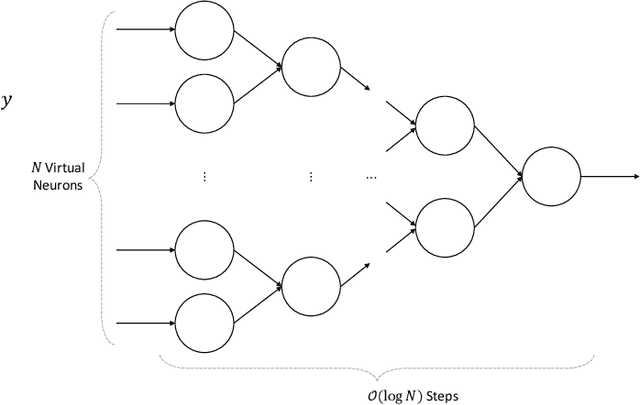
Neuromorphic computers perform computations by emulating the human brain, and use extremely low power. They are expected to be indispensable for energy-efficient computing in the future. While they are primarily used in spiking neural network-based machine learning applications, neuromorphic computers are known to be Turing-complete, and thus, capable of general-purpose computation. However, to fully realize their potential for general-purpose, energy-efficient computing, it is important to devise efficient mechanisms for encoding numbers. Current encoding approaches have limited applicability and may not be suitable for general-purpose computation. In this paper, we present the virtual neuron as an encoding mechanism for integers and rational numbers. We evaluate the performance of the virtual neuron on physical and simulated neuromorphic hardware and show that it can perform an addition operation using 23 nJ of energy on average using a mixed-signal memristor-based neuromorphic processor. We also demonstrate its utility by using it in some of the mu-recursive functions, which are the building blocks of general-purpose computation.

Neuromorphic Computing is Turing-Complete

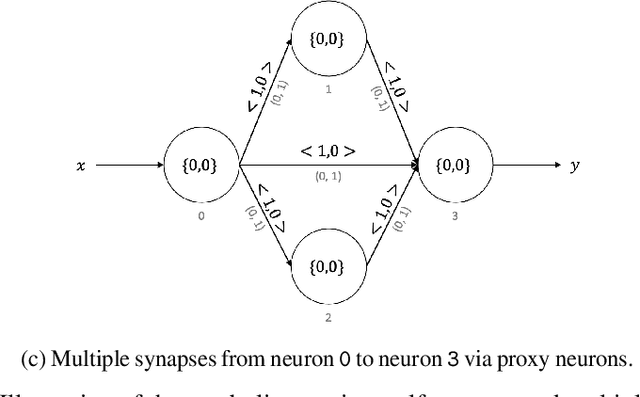
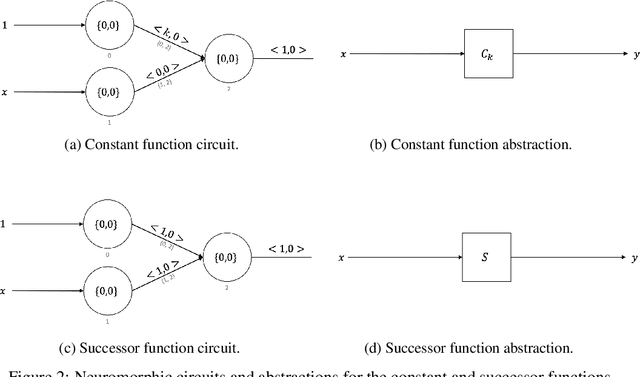
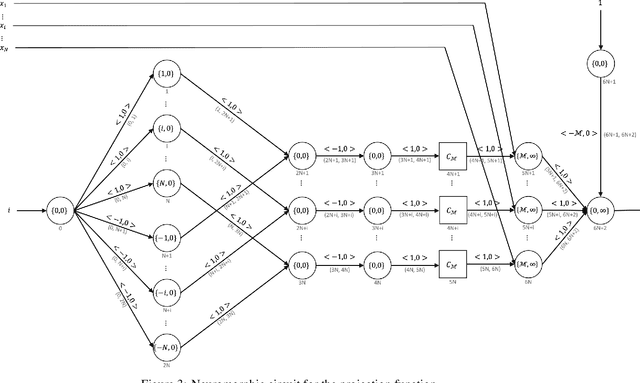
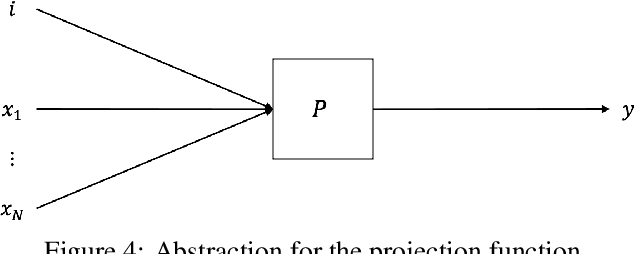
Neuromorphic computing is a non-von Neumann computing paradigm that performs computation by emulating the human brain. Neuromorphic systems are extremely energy-efficient and known to consume thousands of times less power than CPUs and GPUs. They have the potential to drive critical use cases such as autonomous vehicles, edge computing and internet of things in the future. For this reason, they are sought to be an indispensable part of the future computing landscape. Neuromorphic systems are mainly used for spike-based machine learning applications, although there are some non-machine learning applications in graph theory, differential equations, and spike-based simulations. These applications suggest that neuromorphic computing might be capable of general-purpose computing. However, general-purpose computability of neuromorphic computing has not been established yet. In this work, we prove that neuromorphic computing is Turing-complete and therefore capable of general-purpose computing. Specifically, we present a model of neuromorphic computing, with just two neuron parameters (threshold and leak), and two synaptic parameters (weight and delay). We devise neuromorphic circuits for computing all the {\mu}-recursive functions (i.e., constant, successor and projection functions) and all the {\mu}-recursive operators (i.e., composition, primitive recursion and minimization operators). Given that the {\mu}-recursive functions and operators are precisely the ones that can be computed using a Turing machine, this work establishes the Turing-completeness of neuromorphic computing.

Adiabatic Quantum Linear Regression

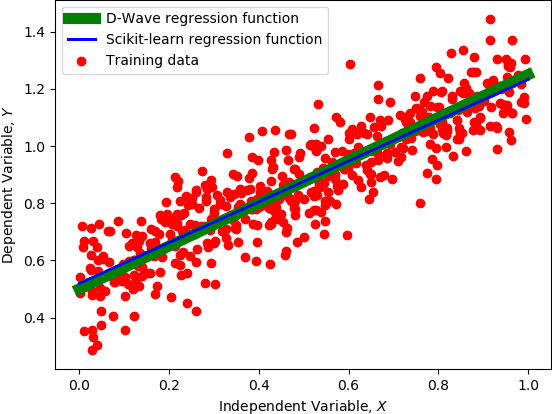
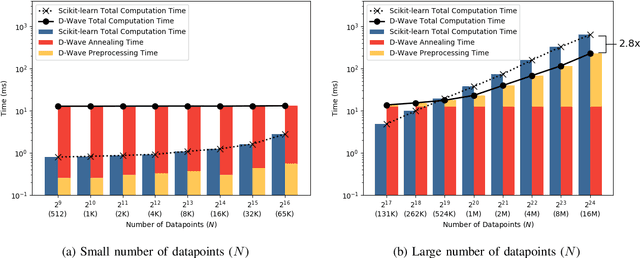
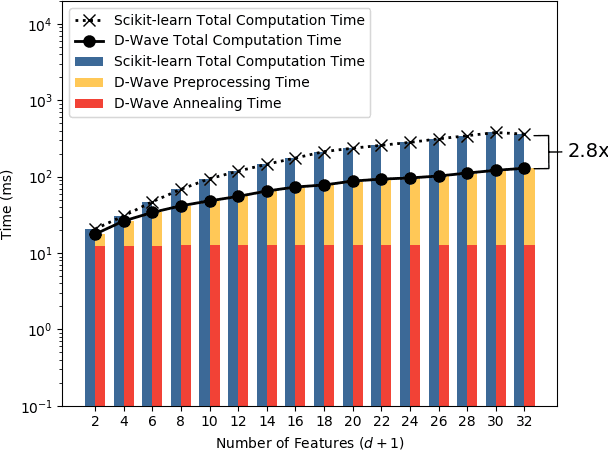
A major challenge in machine learning is the computational expense of training these models. Model training can be viewed as a form of optimization used to fit a machine learning model to a set of data, which can take up significant amount of time on classical computers. Adiabatic quantum computers have been shown to excel at solving optimization problems, and therefore, we believe, present a promising alternative to improve machine learning training times. In this paper, we present an adiabatic quantum computing approach for training a linear regression model. In order to do this, we formulate the regression problem as a quadratic unconstrained binary optimization (QUBO) problem. We analyze our quantum approach theoretically, test it on the D-Wave 2000Q adiabatic quantum computer and compare its performance to a classical approach that uses the Scikit-learn library in Python. Our analysis shows that the quantum approach attains up to 2.8x speedup over the classical approach on larger datasets, and performs at par with the classical approach on the regression error metric.