Non-smooth Bayesian Optimization in Tuning Problems
Paper and Code
Sep 15, 2021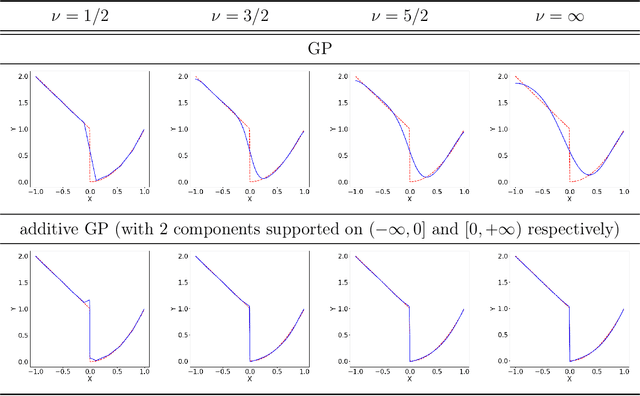

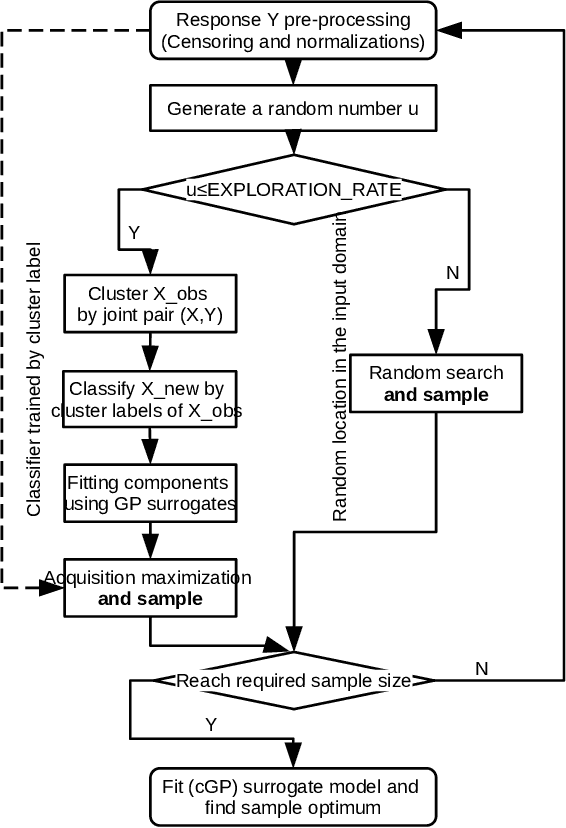
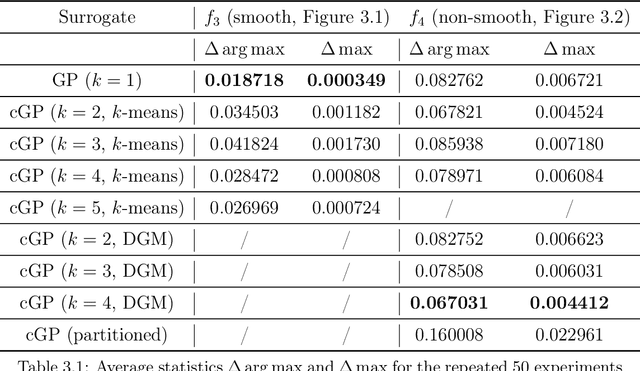
Building surrogate models is one common approach when we attempt to learn unknown black-box functions. Bayesian optimization provides a framework which allows us to build surrogate models based on sequential samples drawn from the function and find the optimum. Tuning algorithmic parameters to optimize the performance of large, complicated "black-box" application codes is a specific important application, which aims at finding the optima of black-box functions. Within the Bayesian optimization framework, the Gaussian process model produces smooth or continuous sample paths. However, the black-box function in the tuning problem is often non-smooth. This difficult tuning problem is worsened by the fact that we usually have limited sequential samples from the black-box function. Motivated by these issues encountered in tuning, we propose a novel additive Gaussian process model called clustered Gaussian process (cGP), where the additive components are induced by clustering. In the examples we studied, the performance can be improved by as much as 90% among repetitive experiments. By using this surrogate model, we want to capture the non-smoothness of the black-box function. In addition to an algorithm for constructing this model, we also apply the model to several artificial and real applications to evaluate it.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge