Implicit Compressibility of Overparametrized Neural Networks Trained with Heavy-Tailed SGD

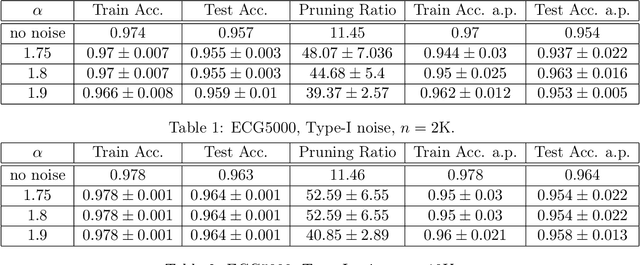
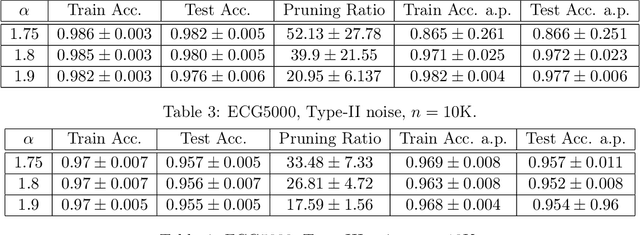
Neural network compression has been an increasingly important subject, due to its practical implications in terms of reducing the computational requirements and its theoretical implications, as there is an explicit connection between compressibility and the generalization error. Recent studies have shown that the choice of the hyperparameters of stochastic gradient descent (SGD) can have an effect on the compressibility of the learned parameter vector. Even though these results have shed some light on the role of the training dynamics over compressibility, they relied on unverifiable assumptions and the resulting theory does not provide a practical guideline due to its implicitness. In this study, we propose a simple modification for SGD, such that the outputs of the algorithm will be provably compressible without making any nontrivial assumptions. We consider a one-hidden-layer neural network trained with SGD and we inject additive heavy-tailed noise to the iterates at each iteration. We then show that, for any compression rate, there exists a level of overparametrization (i.e., the number of hidden units), such that the output of the algorithm will be compressible with high probability. To achieve this result, we make two main technical contributions: (i) we build on a recent study on stochastic analysis and prove a 'propagation of chaos' result with improved rates for a class of heavy-tailed stochastic differential equations, and (ii) we derive strong-error estimates for their Euler discretization. We finally illustrate our approach on experiments, where the results suggest that the proposed approach achieves compressibility with a slight compromise from the training and test error.

Federated Learning You May Communicate Less Often!

We investigate the generalization error of statistical learning models in a Federated Learning (FL) setting. Specifically, we study the evolution of the generalization error with the number of communication rounds between the clients and the parameter server, i.e., the effect on the generalization error of how often the local models as computed by the clients are aggregated at the parameter server. We establish PAC-Bayes and rate-distortion theoretic bounds on the generalization error that account explicitly for the effect of the number of rounds, say $ R \in \mathbb{N}$, in addition to the number of participating devices $K$ and individual datasets size $n$. The bounds, which apply in their generality for a large class of loss functions and learning algorithms, appear to be the first of their kind for the FL setting. Furthermore, we apply our bounds to FL-type Support Vector Machines (FSVM); and we derive (more) explicit bounds on the generalization error in this case. In particular, we show that the generalization error of FSVM increases with $R$, suggesting that more frequent communication with the parameter server diminishes the generalization power of such learning algorithms. Combined with that the empirical risk generally decreases for larger values of $R$, this indicates that $R$ might be a parameter to optimize in order to minimize the population risk of FL algorithms. Moreover, specialized to the case $R=1$ (sometimes referred to as "one-shot" FL or distributed learning) our bounds suggest that the generalization error of the FL setting decreases faster than that of centralized learning by a factor of $\mathcal{O}(\sqrt{\log(K)/K})$, thereby generalizing recent findings in this direction to arbitrary loss functions and algorithms. The results of this paper are also validated on some experiments.

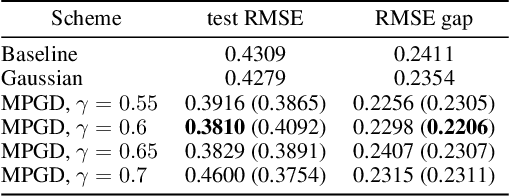
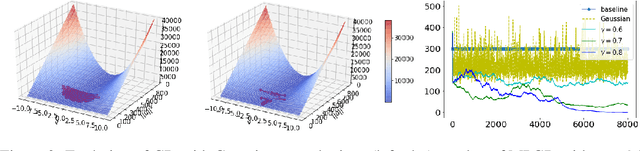
Chaotic Regularization and Heavy-Tailed Limits for Deterministic Gradient Descent

Recent studies have shown that gradient descent (GD) can achieve improved generalization when its dynamics exhibits a chaotic behavior. However, to obtain the desired effect, the step-size should be chosen sufficiently large, a task which is problem dependent and can be difficult in practice. In this study, we incorporate a chaotic component to GD in a controlled manner, and introduce multiscale perturbed GD (MPGD), a novel optimization framework where the GD recursion is augmented with chaotic perturbations that evolve via an independent dynamical system. We analyze MPGD from three different angles: (i) By building up on recent advances in rough paths theory, we show that, under appropriate assumptions, as the step-size decreases, the MPGD recursion converges weakly to a stochastic differential equation (SDE) driven by a heavy-tailed L\'evy-stable process. (ii) By making connections to recently developed generalization bounds for heavy-tailed processes, we derive a generalization bound for the limiting SDE and relate the worst-case generalization error over the trajectories of the process to the parameters of MPGD. (iii) We analyze the implicit regularization effect brought by the dynamical regularization and show that, in the weak perturbation regime, MPGD introduces terms that penalize the Hessian of the loss function. Empirical results are provided to demonstrate the advantages of MPGD.