Heterogeneity Matters even More in Distributed Learning: Study from Generalization Perspective

In this paper, we investigate the effect of data heterogeneity across clients on the performance of distributed learning systems, i.e., one-round Federated Learning, as measured by the associated generalization error. Specifically, \(K\) clients have each \(n\) training samples generated independently according to a possibly different data distribution and their individually chosen models are aggregated by a central server. We study the effect of the discrepancy between the clients' data distributions on the generalization error of the aggregated model. First, we establish in-expectation and tail upper bounds on the generalization error in terms of the distributions. In part, the bounds extend the popular Conditional Mutual Information (CMI) bound which was developed for the centralized learning setting, i.e., \(K=1\), to the distributed learning setting with arbitrary number of clients $K \geq 1$. Then, we use a connection with information theoretic rate-distortion theory to derive possibly tighter \textit{lossy} versions of these bounds. Next, we apply our lossy bounds to study the effect of data heterogeneity across clients on the generalization error for distributed classification problem in which each client uses Support Vector Machines (D-SVM). In this case, we establish explicit generalization error bounds which depend explicitly on the data heterogeneity degree. It is shown that the bound gets smaller as the degree of data heterogeneity across clients gets higher, thereby suggesting that D-SVM generalizes better when the dissimilarity between the clients' training samples is bigger. This finding, which goes beyond D-SVM, is validated experimentally through a number of experiments.

Federated Learning You May Communicate Less Often!

We investigate the generalization error of statistical learning models in a Federated Learning (FL) setting. Specifically, we study the evolution of the generalization error with the number of communication rounds between the clients and the parameter server, i.e., the effect on the generalization error of how often the local models as computed by the clients are aggregated at the parameter server. We establish PAC-Bayes and rate-distortion theoretic bounds on the generalization error that account explicitly for the effect of the number of rounds, say $ R \in \mathbb{N}$, in addition to the number of participating devices $K$ and individual datasets size $n$. The bounds, which apply in their generality for a large class of loss functions and learning algorithms, appear to be the first of their kind for the FL setting. Furthermore, we apply our bounds to FL-type Support Vector Machines (FSVM); and we derive (more) explicit bounds on the generalization error in this case. In particular, we show that the generalization error of FSVM increases with $R$, suggesting that more frequent communication with the parameter server diminishes the generalization power of such learning algorithms. Combined with that the empirical risk generally decreases for larger values of $R$, this indicates that $R$ might be a parameter to optimize in order to minimize the population risk of FL algorithms. Moreover, specialized to the case $R=1$ (sometimes referred to as "one-shot" FL or distributed learning) our bounds suggest that the generalization error of the FL setting decreases faster than that of centralized learning by a factor of $\mathcal{O}(\sqrt{\log(K)/K})$, thereby generalizing recent findings in this direction to arbitrary loss functions and algorithms. The results of this paper are also validated on some experiments.

More Communication Does Not Result in Smaller Generalization Error in Federated Learning

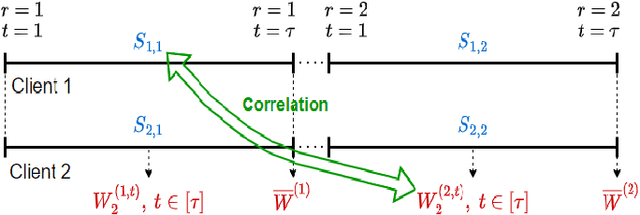
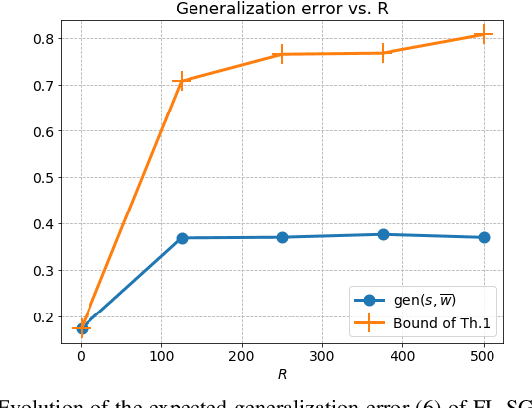
We study the generalization error of statistical learning models in a Federated Learning (FL) setting. Specifically, there are $K$ devices or clients, each holding an independent own dataset of size $n$. Individual models, learned locally via Stochastic Gradient Descent, are aggregated (averaged) by a central server into a global model and then sent back to the devices. We consider multiple (say $R \in \mathbb N^*$) rounds of model aggregation and study the effect of $R$ on the generalization error of the final aggregated model. We establish an upper bound on the generalization error that accounts explicitly for the effect of $R$ (in addition to the number of participating devices $K$ and dataset size $n$). It is observed that, for fixed $(n, K)$, the bound increases with $R$, suggesting that the generalization of such learning algorithms is negatively affected by more frequent communication with the parameter server. Combined with the fact that the empirical risk, however, generally decreases for larger values of $R$, this indicates that $R$ might be a parameter to optimize to reduce the population risk of FL algorithms. The results of this paper, which extend straightforwardly to the heterogeneous data setting, are also illustrated through numerical examples.

Rate-Distortion Theoretic Bounds on Generalization Error for Distributed Learning

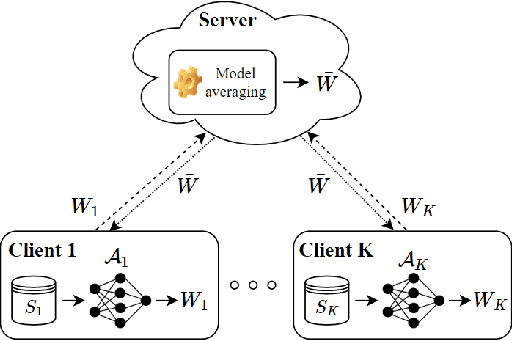
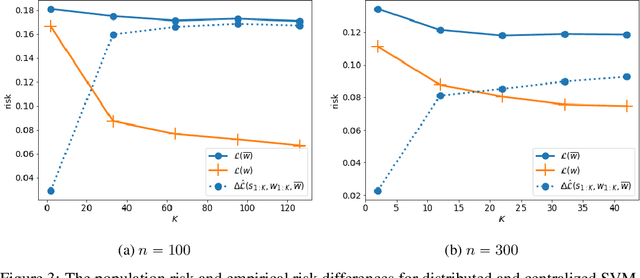
In this paper, we use tools from rate-distortion theory to establish new upper bounds on the generalization error of statistical distributed learning algorithms. Specifically, there are $K$ clients whose individually chosen models are aggregated by a central server. The bounds depend on the compressibility of each client's algorithm while keeping other clients' algorithms un-compressed, and leverage the fact that small changes in each local model change the aggregated model by a factor of only $1/K$. Adopting a recently proposed approach by Sefidgaran et al., and extending it suitably to the distributed setting, this enables smaller rate-distortion terms which are shown to translate into tighter generalization bounds. The bounds are then applied to the distributed support vector machines (SVM), suggesting that the generalization error of the distributed setting decays faster than that of the centralized one with a factor of $\mathcal{O}(\log(K)/\sqrt{K})$. This finding is validated also experimentally. A similar conclusion is obtained for a multiple-round federated learning setup where each client uses stochastic gradient Langevin dynamics (SGLD).