Rate-Distortion Theoretic Bounds on Generalization Error for Distributed Learning
Paper and Code
Jun 06, 2022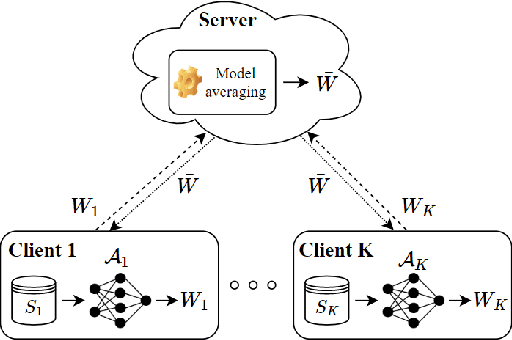
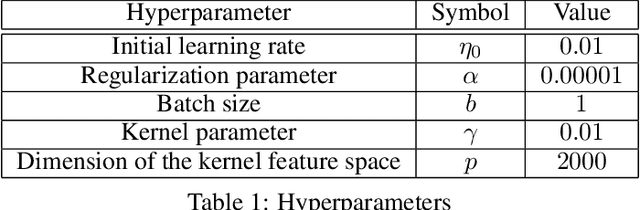

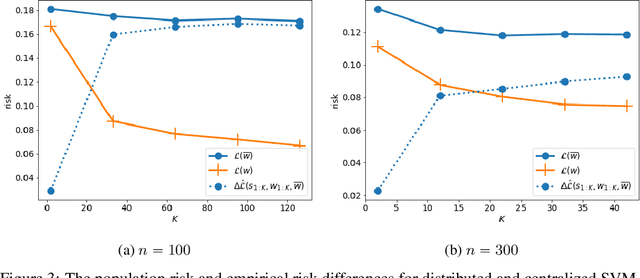
In this paper, we use tools from rate-distortion theory to establish new upper bounds on the generalization error of statistical distributed learning algorithms. Specifically, there are $K$ clients whose individually chosen models are aggregated by a central server. The bounds depend on the compressibility of each client's algorithm while keeping other clients' algorithms un-compressed, and leverage the fact that small changes in each local model change the aggregated model by a factor of only $1/K$. Adopting a recently proposed approach by Sefidgaran et al., and extending it suitably to the distributed setting, this enables smaller rate-distortion terms which are shown to translate into tighter generalization bounds. The bounds are then applied to the distributed support vector machines (SVM), suggesting that the generalization error of the distributed setting decays faster than that of the centralized one with a factor of $\mathcal{O}(\log(K)/\sqrt{K})$. This finding is validated also experimentally. A similar conclusion is obtained for a multiple-round federated learning setup where each client uses stochastic gradient Langevin dynamics (SGLD).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge