Heterogeneity Matters even More in Distributed Learning: Study from Generalization Perspective

In this paper, we investigate the effect of data heterogeneity across clients on the performance of distributed learning systems, i.e., one-round Federated Learning, as measured by the associated generalization error. Specifically, \(K\) clients have each \(n\) training samples generated independently according to a possibly different data distribution and their individually chosen models are aggregated by a central server. We study the effect of the discrepancy between the clients' data distributions on the generalization error of the aggregated model. First, we establish in-expectation and tail upper bounds on the generalization error in terms of the distributions. In part, the bounds extend the popular Conditional Mutual Information (CMI) bound which was developed for the centralized learning setting, i.e., \(K=1\), to the distributed learning setting with arbitrary number of clients $K \geq 1$. Then, we use a connection with information theoretic rate-distortion theory to derive possibly tighter \textit{lossy} versions of these bounds. Next, we apply our lossy bounds to study the effect of data heterogeneity across clients on the generalization error for distributed classification problem in which each client uses Support Vector Machines (D-SVM). In this case, we establish explicit generalization error bounds which depend explicitly on the data heterogeneity degree. It is shown that the bound gets smaller as the degree of data heterogeneity across clients gets higher, thereby suggesting that D-SVM generalizes better when the dissimilarity between the clients' training samples is bigger. This finding, which goes beyond D-SVM, is validated experimentally through a number of experiments.

Generalization Guarantees for Representation Learning via Data-Dependent Gaussian Mixture Priors

We establish in-expectation and tail bounds on the generalization error of representation learning type algorithms. The bounds are in terms of the relative entropy between the distribution of the representations extracted from the training and "test'' datasets and a data-dependent symmetric prior, i.e., the Minimum Description Length (MDL) of the latent variables for the training and test datasets. Our bounds are shown to reflect the "structure" and "simplicity'' of the encoder and significantly improve upon the few existing ones for the studied model. We then use our in-expectation bound to devise a suitable data-dependent regularizer; and we investigate thoroughly the important question of the selection of the prior. We propose a systematic approach to simultaneously learning a data-dependent Gaussian mixture prior and using it as a regularizer. Interestingly, we show that a weighted attention mechanism emerges naturally in this procedure. Our experiments show that our approach outperforms the now popular Variational Information Bottleneck (VIB) method as well as the recent Category-Dependent VIB (CDVIB).

Minimal Communication-Cost Statistical Learning

A client device which has access to $n$ training data samples needs to obtain a statistical hypothesis or model $W$ and then to send it to a remote server. The client and the server devices share some common randomness sequence as well as a prior on the hypothesis space. In this problem a suitable hypothesis or model $W$ should meet two distinct design criteria simultaneously: (i) small (population) risk during the inference phase and (ii) small 'complexity' for it to be conveyed to the server with minimum communication cost. In this paper, we propose a joint training and source coding scheme with provable in-expectation guarantees, where the expectation is over the encoder's output message. Specifically, we show that by imposing a constraint on a suitable Kullback-Leibler divergence between the conditional distribution induced by a compressed learning model $\widehat{W}$ given $W$ and the prior, one guarantees simultaneously small average empirical risk (aka training loss), small average generalization error and small average communication cost. We also consider a one-shot scenario in which the guarantees on the empirical risk and generalization error are obtained for every encoder's output message.

Minimum Description Length and Generalization Guarantees for Representation Learning

A major challenge in designing efficient statistical supervised learning algorithms is finding representations that perform well not only on available training samples but also on unseen data. While the study of representation learning has spurred much interest, most existing such approaches are heuristic; and very little is known about theoretical generalization guarantees. In this paper, we establish a compressibility framework that allows us to derive upper bounds on the generalization error of a representation learning algorithm in terms of the "Minimum Description Length" (MDL) of the labels or the latent variables (representations). Rather than the mutual information between the encoder's input and the representation, which is often believed to reflect the algorithm's generalization capability in the related literature but in fact, falls short of doing so, our new bounds involve the "multi-letter" relative entropy between the distribution of the representations (or labels) of the training and test sets and a fixed prior. In particular, these new bounds reflect the structure of the encoder and are not vacuous for deterministic algorithms. Our compressibility approach, which is information-theoretic in nature, builds upon that of Blum-Langford for PAC-MDL bounds and introduces two essential ingredients: block-coding and lossy-compression. The latter allows our approach to subsume the so-called geometrical compressibility as a special case. To the best knowledge of the authors, the established generalization bounds are the first of their kind for Information Bottleneck (IB) type encoders and representation learning. Finally, we partly exploit the theoretical results by introducing a new data-dependent prior. Numerical simulations illustrate the advantages of well-chosen such priors over classical priors used in IB.

Implicit Compressibility of Overparametrized Neural Networks Trained with Heavy-Tailed SGD

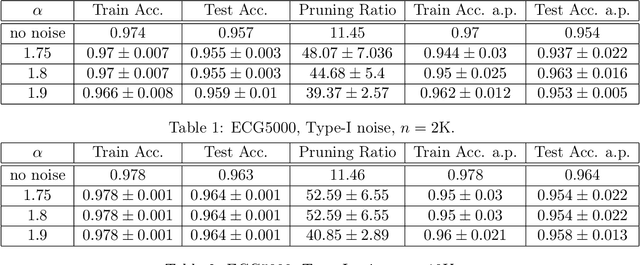
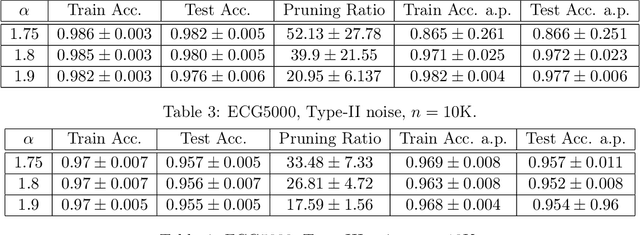
Neural network compression has been an increasingly important subject, due to its practical implications in terms of reducing the computational requirements and its theoretical implications, as there is an explicit connection between compressibility and the generalization error. Recent studies have shown that the choice of the hyperparameters of stochastic gradient descent (SGD) can have an effect on the compressibility of the learned parameter vector. Even though these results have shed some light on the role of the training dynamics over compressibility, they relied on unverifiable assumptions and the resulting theory does not provide a practical guideline due to its implicitness. In this study, we propose a simple modification for SGD, such that the outputs of the algorithm will be provably compressible without making any nontrivial assumptions. We consider a one-hidden-layer neural network trained with SGD and we inject additive heavy-tailed noise to the iterates at each iteration. We then show that, for any compression rate, there exists a level of overparametrization (i.e., the number of hidden units), such that the output of the algorithm will be compressible with high probability. To achieve this result, we make two main technical contributions: (i) we build on a recent study on stochastic analysis and prove a 'propagation of chaos' result with improved rates for a class of heavy-tailed stochastic differential equations, and (ii) we derive strong-error estimates for their Euler discretization. We finally illustrate our approach on experiments, where the results suggest that the proposed approach achieves compressibility with a slight compromise from the training and test error.

Federated Learning You May Communicate Less Often!

We investigate the generalization error of statistical learning models in a Federated Learning (FL) setting. Specifically, we study the evolution of the generalization error with the number of communication rounds between the clients and the parameter server, i.e., the effect on the generalization error of how often the local models as computed by the clients are aggregated at the parameter server. We establish PAC-Bayes and rate-distortion theoretic bounds on the generalization error that account explicitly for the effect of the number of rounds, say $ R \in \mathbb{N}$, in addition to the number of participating devices $K$ and individual datasets size $n$. The bounds, which apply in their generality for a large class of loss functions and learning algorithms, appear to be the first of their kind for the FL setting. Furthermore, we apply our bounds to FL-type Support Vector Machines (FSVM); and we derive (more) explicit bounds on the generalization error in this case. In particular, we show that the generalization error of FSVM increases with $R$, suggesting that more frequent communication with the parameter server diminishes the generalization power of such learning algorithms. Combined with that the empirical risk generally decreases for larger values of $R$, this indicates that $R$ might be a parameter to optimize in order to minimize the population risk of FL algorithms. Moreover, specialized to the case $R=1$ (sometimes referred to as "one-shot" FL or distributed learning) our bounds suggest that the generalization error of the FL setting decreases faster than that of centralized learning by a factor of $\mathcal{O}(\sqrt{\log(K)/K})$, thereby generalizing recent findings in this direction to arbitrary loss functions and algorithms. The results of this paper are also validated on some experiments.

More Communication Does Not Result in Smaller Generalization Error in Federated Learning

We study the generalization error of statistical learning models in a Federated Learning (FL) setting. Specifically, there are $K$ devices or clients, each holding an independent own dataset of size $n$. Individual models, learned locally via Stochastic Gradient Descent, are aggregated (averaged) by a central server into a global model and then sent back to the devices. We consider multiple (say $R \in \mathbb N^*$) rounds of model aggregation and study the effect of $R$ on the generalization error of the final aggregated model. We establish an upper bound on the generalization error that accounts explicitly for the effect of $R$ (in addition to the number of participating devices $K$ and dataset size $n$). It is observed that, for fixed $(n, K)$, the bound increases with $R$, suggesting that the generalization of such learning algorithms is negatively affected by more frequent communication with the parameter server. Combined with the fact that the empirical risk, however, generally decreases for larger values of $R$, this indicates that $R$ might be a parameter to optimize to reduce the population risk of FL algorithms. The results of this paper, which extend straightforwardly to the heterogeneous data setting, are also illustrated through numerical examples.

Data-dependent Generalization Bounds via Variable-Size Compressibility

In this paper, we establish novel data-dependent upper bounds on the generalization error through the lens of a "variable-size compressibility" framework that we introduce newly here. In this framework, the generalization error of an algorithm is linked to a variable-size 'compression rate' of its input data. This is shown to yield bounds that depend on the empirical measure of the given input data at hand, rather than its unknown distribution. Our new generalization bounds that we establish are tail bounds, tail bounds on the expectation, and in-expectations bounds. Moreover, it is shown that our framework also allows to derive general bounds on any function of the input data and output hypothesis random variables. In particular, these general bounds are shown to subsume and possibly improve over several existing PAC-Bayes and data-dependent intrinsic dimension-based bounds that are recovered as special cases, thus unveiling a unifying character of our approach. For instance, a new data-dependent intrinsic dimension based bounds is established, which connects the generalization error to the optimization trajectories and reveals various interesting connections with rate-distortion dimension of process, R\'enyi information dimension of process, and metric mean dimension.

Rate-Distortion Theoretic Bounds on Generalization Error for Distributed Learning

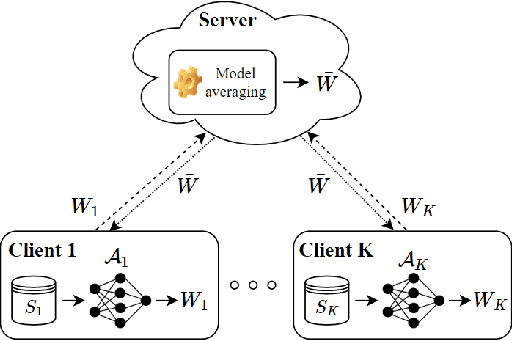
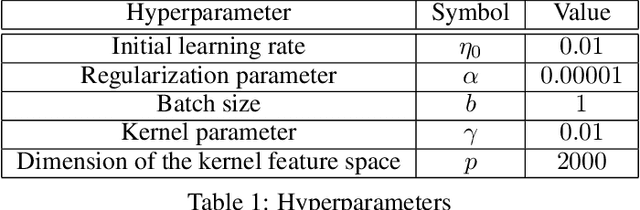
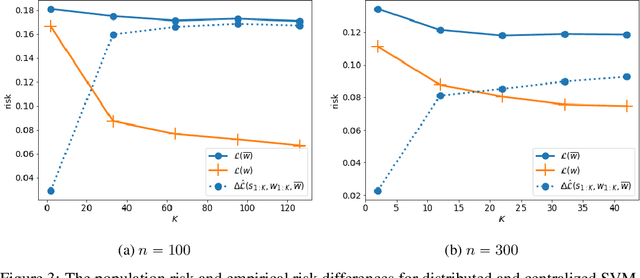
In this paper, we use tools from rate-distortion theory to establish new upper bounds on the generalization error of statistical distributed learning algorithms. Specifically, there are $K$ clients whose individually chosen models are aggregated by a central server. The bounds depend on the compressibility of each client's algorithm while keeping other clients' algorithms un-compressed, and leverage the fact that small changes in each local model change the aggregated model by a factor of only $1/K$. Adopting a recently proposed approach by Sefidgaran et al., and extending it suitably to the distributed setting, this enables smaller rate-distortion terms which are shown to translate into tighter generalization bounds. The bounds are then applied to the distributed support vector machines (SVM), suggesting that the generalization error of the distributed setting decays faster than that of the centralized one with a factor of $\mathcal{O}(\log(K)/\sqrt{K})$. This finding is validated also experimentally. A similar conclusion is obtained for a multiple-round federated learning setup where each client uses stochastic gradient Langevin dynamics (SGLD).

In-Network Learning: Distributed Training and Inference in Networks

It is widely perceived that leveraging the success of modern machine learning techniques to mobile devices and wireless networks has the potential of enabling important new services. This, however, poses significant challenges, essentially due to that both data and processing power are highly distributed in a wireless network. In this paper, we develop a learning algorithm and an architecture that make use of multiple data streams and processing units, not only during the training phase but also during the inference phase. In particular, the analysis reveals how inference propagates and fuses across a network. We study the design criterion of our proposed method and its bandwidth requirements. Also, we discuss implementation aspects using neural networks in typical wireless radio access; and provide experiments that illustrate benefits over state-of-the-art techniques.