Analyzing Deep Transformer Models for Time Series Forecasting via Manifold Learning

Transformer models have consistently achieved remarkable results in various domains such as natural language processing and computer vision. However, despite ongoing research efforts to better understand these models, the field still lacks a comprehensive understanding. This is particularly true for deep time series forecasting methods, where analysis and understanding work is relatively limited. Time series data, unlike image and text information, can be more challenging to interpret and analyze. To address this, we approach the problem from a manifold learning perspective, assuming that the latent representations of time series forecasting models lie next to a low-dimensional manifold. In our study, we focus on analyzing the geometric features of these latent data manifolds, including intrinsic dimension and principal curvatures. Our findings reveal that deep transformer models exhibit similar geometric behavior across layers, and these geometric features are correlated with model performance. Additionally, we observe that untrained models initially have different structures, but they rapidly converge during training. By leveraging our geometric analysis and differentiable tools, we can potentially design new and improved deep forecasting neural networks. This approach complements existing analysis studies and contributes to a better understanding of transformer models in the context of time series forecasting. Code is released at https://github.com/azencot-group/GATLM.

First-Order Manifold Data Augmentation for Regression Learning

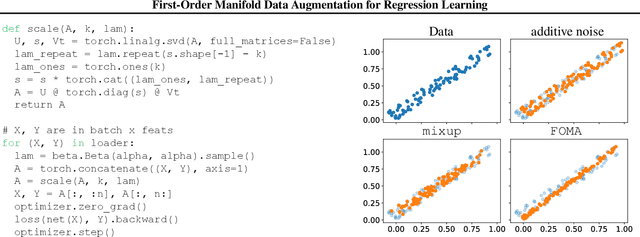
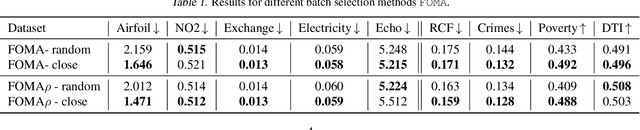
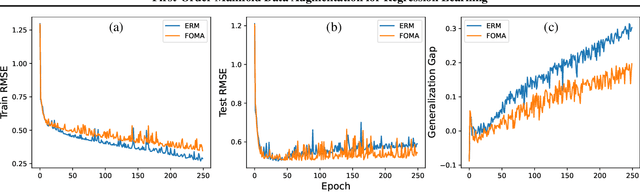
Data augmentation (DA) methods tailored to specific domains generate synthetic samples by applying transformations that are appropriate for the characteristics of the underlying data domain, such as rotations on images and time warping on time series data. In contrast, domain-independent approaches, e.g. mixup, are applicable to various data modalities, and as such they are general and versatile. While regularizing classification tasks via DA is a well-explored research topic, the effect of DA on regression problems received less attention. To bridge this gap, we study the problem of domain-independent augmentation for regression, and we introduce FOMA: a new data-driven domain-independent data augmentation method. Essentially, our approach samples new examples from the tangent planes of the train distribution. Augmenting data in this way aligns with the network tendency towards capturing the dominant features of its input signals. We evaluate FOMA on in-distribution generalization and out-of-distribution robustness benchmarks, and we show that it improves the generalization of several neural architectures. We also find that strong baselines based on mixup are less effective in comparison to our approach. Our code is publicly available athttps://github.com/azencot-group/FOMA.