Physics-Informed Machine Learning for Seismic Response Prediction OF Nonlinear Steel Moment Resisting Frame Structures
Paper and Code
Mar 01, 2024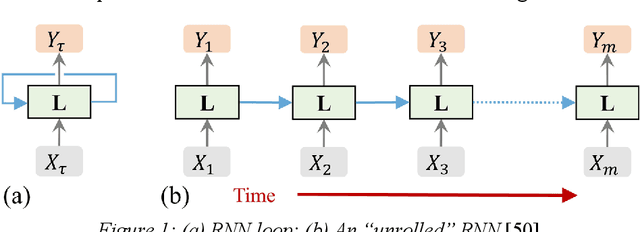
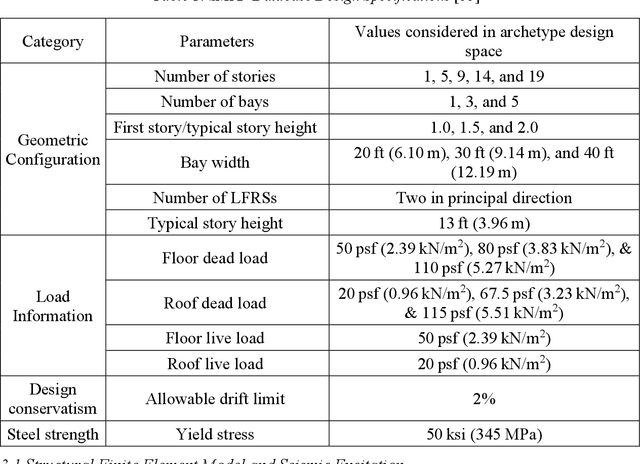
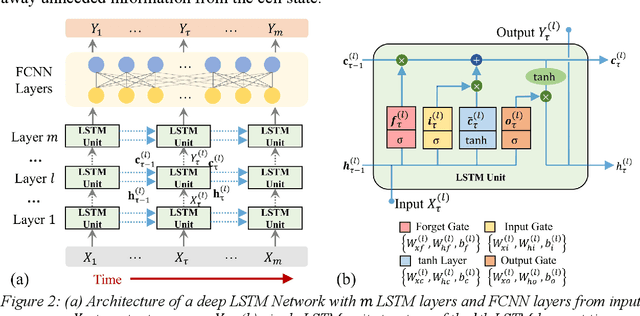
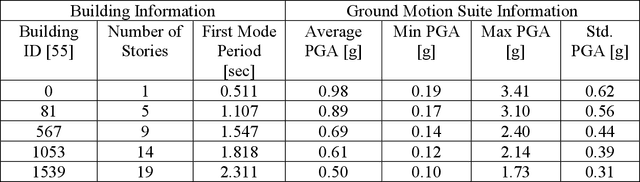
There is a growing interest in utilizing machine learning (ML) methods for structural metamodeling due to the substantial computational cost of traditional numerical simulations. The existing data-driven strategies show potential limitations to the model robustness and interpretability as well as the dependency of rich data. To address these challenges, this paper presents a novel physics-informed machine learning (PiML) method, which incorporates scientific principles and physical laws into deep neural networks for modeling seismic responses of nonlinear structures. The basic concept is to constrain the solution space of the ML model within known physical bounds. This is made possible with three main features, namely, model order reduction, a long short-term memory (LSTM) networks, and Newton's second law (e.g., the equation of motion). Model order reduction is essential for handling structural systems with inherent redundancy and enhancing model efficiency. The LSTM network captures temporal dependencies, enabling accurate prediction of time series responses. The equation of motion is manipulated to learn system nonlinearities and confines the solution space within physically interpretable results. These features enable model training with relatively sparse data and offer benefits in terms of accuracy, interpretability, and robustness. Furthermore, a dataset of seismically designed archetype ductile planar steel moment resistant frames under horizontal seismic loading, available in the DesignSafe-CI Database, is considered for evaluation of the proposed method. The resulting metamodel is capable of handling more complex data compared to existing physics-guided LSTM models and outperforms other non-physics data-driven neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge