A Machine Learning Approach Capturing Hidden Parameters in Autonomous Thin-Film Deposition

The integration of machine learning and robotics into thin film deposition is transforming material discovery and optimization. However, challenges remain in achieving a fully autonomous cycle of deposition, characterization, and decision-making. Additionally, the inherent sensitivity of thin film growth to hidden parameters such as substrate conditions and chamber conditions can compromise the performance of machine learning models. In this work, we demonstrate a fully autonomous physical vapor deposition system that combines in-situ optical spectroscopy, a high-throughput robotic sample handling system, and Gaussian Process Regression models. By employing a calibration layer to account for hidden parameter variations and an active learning algorithm to optimize the exploration of the parameter space, the system fabricates silver thin films with optical reflected power ratios within 2.5% of the target in an average of 2.3 attempts. This approach significantly reduces the time and labor required for thin film deposition, showcasing the potential of machine learning-driven automation in accelerating material development.

Constrained Multi-objective Bayesian Optimization through Optimistic Constraints Estimation

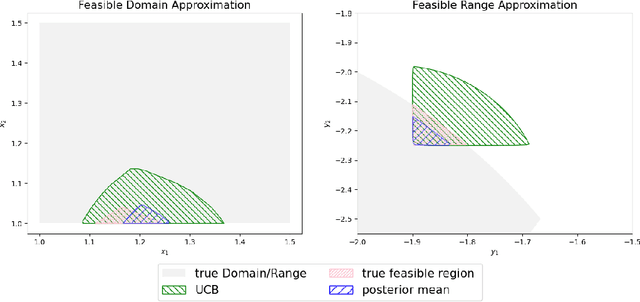
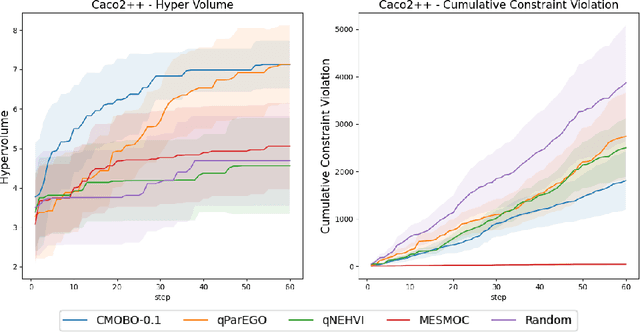
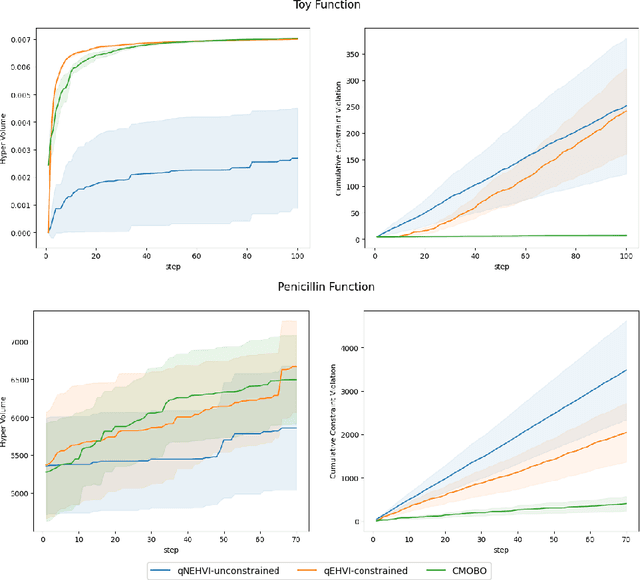
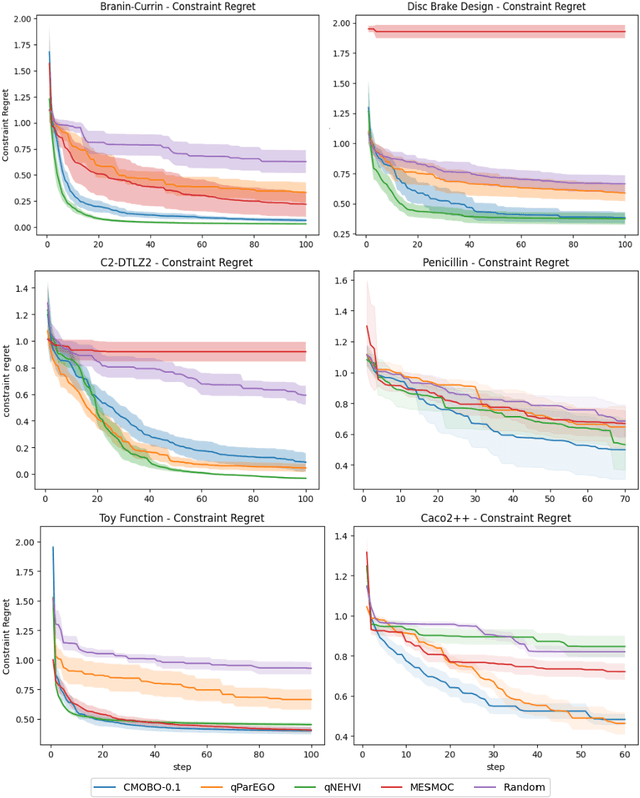
Multi-objective Bayesian optimization has been widely adopted in scientific experiment design, including drug discovery and hyperparameter optimization. In practice, regulatory or safety concerns often impose additional thresholds on certain attributes of the experimental outcomes. Previous work has primarily focused on constrained single-objective optimization tasks or active search under constraints. We propose CMOBO, a sample-efficient constrained multi-objective Bayesian optimization algorithm that balances learning of the feasible region (defined on multiple unknowns) with multi-objective optimization within the feasible region in a principled manner. We provide both theoretical justification and empirical evidence, demonstrating the efficacy of our approach on various synthetic benchmarks and real-world applications.

No-Regret Learning of Nash Equilibrium for Black-Box Games via Gaussian Processes

This paper investigates the challenge of learning in black-box games, where the underlying utility function is unknown to any of the agents. While there is an extensive body of literature on the theoretical analysis of algorithms for computing the Nash equilibrium with complete information about the game, studies on Nash equilibrium in black-box games are less common. In this paper, we focus on learning the Nash equilibrium when the only available information about an agent's payoff comes in the form of empirical queries. We provide a no-regret learning algorithm that utilizes Gaussian processes to identify the equilibrium in such games. Our approach not only ensures a theoretical convergence rate but also demonstrates effectiveness across a variety collection of games through experimental validation.

Constrained Bayesian Optimization with Adaptive Active Learning of Unknown Constraints

Optimizing objectives under constraints, where both the objectives and constraints are black box functions, is a common scenario in real-world applications such as scientific experimental design, design of medical therapies, and industrial process optimization. One popular approach to handling these complex scenarios is Bayesian Optimization (BO). In terms of theoretical behavior, BO is relatively well understood in the unconstrained setting, where its principles have been well explored and validated. However, when it comes to constrained Bayesian optimization (CBO), the existing framework often relies on heuristics or approximations without the same level of theoretical guarantees. In this paper, we delve into the theoretical and practical aspects of constrained Bayesian optimization, where the objective and constraints can be independently evaluated and are subject to noise. By recognizing that both the objective and constraints can help identify high-confidence regions of interest (ROI), we propose an efficient CBO framework that intersects the ROIs identified from each aspect to determine the general ROI. The ROI, coupled with a novel acquisition function that adaptively balances the optimization of the objective and the identification of feasible regions, enables us to derive rigorous theoretical justifications for its performance. We showcase the efficiency and robustness of our proposed CBO framework through empirical evidence and discuss the fundamental challenge of deriving practical regret bounds for CBO algorithms.

Learning Regions of Interest for Bayesian Optimization with Adaptive Level-Set Estimation

We study Bayesian optimization (BO) in high-dimensional and non-stationary scenarios. Existing algorithms for such scenarios typically require extensive hyperparameter tuning, which limits their practical effectiveness. We propose a framework, called BALLET, which adaptively filters for a high-confidence region of interest (ROI) as a superlevel-set of a nonparametric probabilistic model such as a Gaussian process (GP). Our approach is easy to tune, and is able to focus on local region of the optimization space that can be tackled by existing BO methods. The key idea is to use two probabilistic models: a coarse GP to identify the ROI, and a localized GP for optimization within the ROI. We show theoretically that BALLET can efficiently shrink the search space, and can exhibit a tighter regret bound than standard BO without ROI filtering. We demonstrate empirically the effectiveness of BALLET on both synthetic and real-world optimization tasks.

Learning Representation for Bayesian Optimization with Collision-free Regularization

Bayesian optimization has been challenged by datasets with large-scale, high-dimensional, and non-stationary characteristics, which are common in real-world scenarios. Recent works attempt to handle such input by applying neural networks ahead of the classical Gaussian process to learn a latent representation. We show that even with proper network design, such learned representation often leads to collision in the latent space: two points with significantly different observations collide in the learned latent space, leading to degraded optimization performance. To address this issue, we propose LOCo, an efficient deep Bayesian optimization framework which employs a novel regularizer to reduce the collision in the learned latent space and encourage the mapping from the latent space to the objective value to be Lipschitz continuous. LOCo takes in pairs of data points and penalizes those too close in the latent space compared to their target space distance. We provide a rigorous theoretical justification for LOCo by inspecting the regret of this dynamic-embedding-based Bayesian optimization algorithm, where the neural network is iteratively retrained with the regularizer. Our empirical results demonstrate the effectiveness of LOCo on several synthetic and real-world benchmark Bayesian optimization tasks.