Constrained Multi-objective Bayesian Optimization through Optimistic Constraints Estimation
Paper and Code
Nov 06, 2024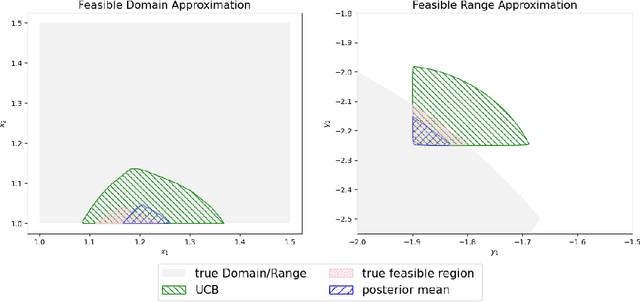
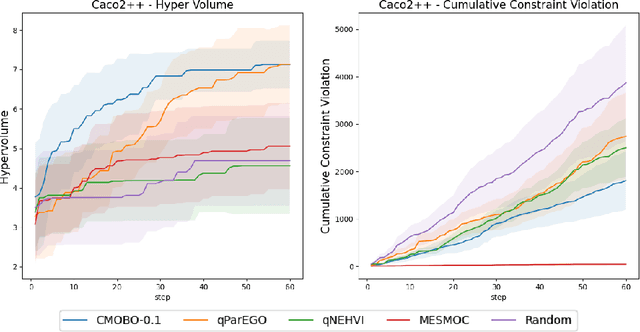
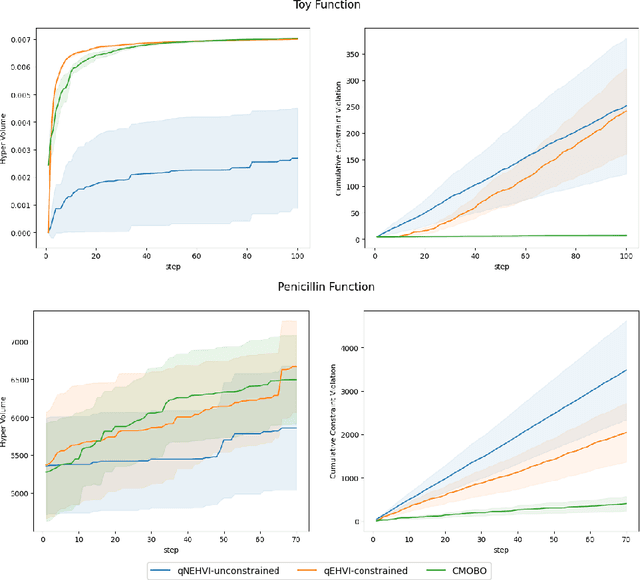
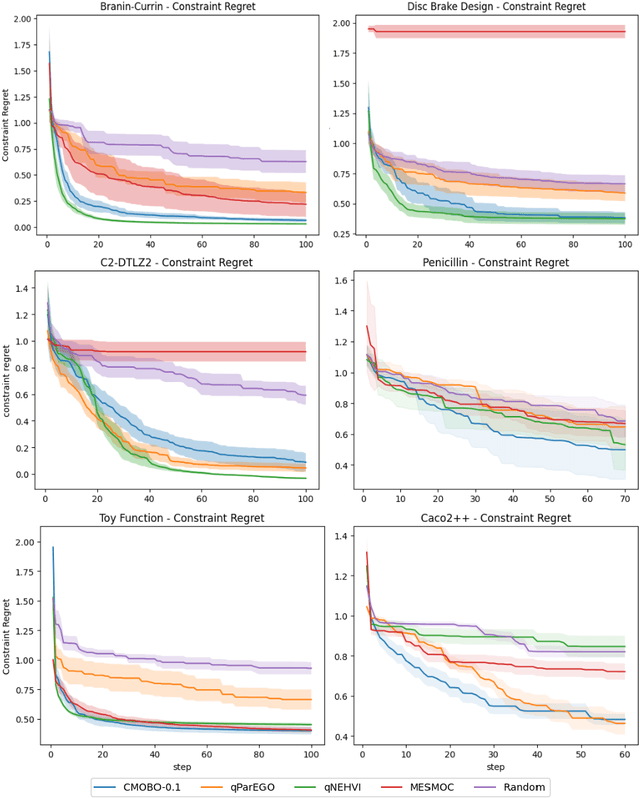
Multi-objective Bayesian optimization has been widely adopted in scientific experiment design, including drug discovery and hyperparameter optimization. In practice, regulatory or safety concerns often impose additional thresholds on certain attributes of the experimental outcomes. Previous work has primarily focused on constrained single-objective optimization tasks or active search under constraints. We propose CMOBO, a sample-efficient constrained multi-objective Bayesian optimization algorithm that balances learning of the feasible region (defined on multiple unknowns) with multi-objective optimization within the feasible region in a principled manner. We provide both theoretical justification and empirical evidence, demonstrating the efficacy of our approach on various synthetic benchmarks and real-world applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge