Deep regularization networks for inverse problems with noisy operators

A supervised learning approach is proposed for regularization of large inverse problems where the main operator is built from noisy data. This is germane to superresolution imaging via the sampling indicators of the inverse scattering theory. We aim to accelerate the spatiotemporal regularization process for this class of inverse problems to enable real-time imaging. In this approach, a neural operator maps each pattern on the right-hand side of the scattering equation to its affiliated regularization parameter. The network is trained in two steps which entails: (1) training on low-resolution regularization maps furnished by the Morozov discrepancy principle with nonoptimal thresholds, and (2) optimizing network predictions through minimization of the Tikhonov loss function regulated by the validation loss. Step 2 allows for tailoring of the approximate maps of Step 1 toward construction of higher quality images. This approach enables direct learning from test data and dispenses with the need for a-priori knowledge of the optimal regularization maps. The network, trained on low-resolution data, quickly generates dense regularization maps for high-resolution imaging. We highlight the importance of the training loss function on the network's generalizability. In particular, we demonstrate that networks informed by the logic of discrepancy principle lead to images of higher contrast. In this case, the training process involves many-objective optimization. We propose a new method to adaptively select the appropriate loss weights during training without requiring an additional optimization process. The proposed approach is synthetically examined for imaging damage evolution in an elastic plate. The results indicate that the discrepancy-informed regularization networks not only accelerate the imaging process, but also remarkably enhance the image quality in complex environments.

Laser Ultrasonic Imaging via the Time Domain Linear Sampling Method

This study investigates the imaging ability of the time-domain linear sampling method (TLSM) when applied to laser ultrasonic (LU) tomography of subsurface defects from limited-aperture measurements. In this vein, the TLSM indicator and it spectral counterpart known as the multifrequency LSM are formulated within the context of LU testing. The affiliated imaging functionals are then computed using synthetic and experimental data germane to LU inspection of aluminum alloy specimens with manufactured defects. Hyperparameters of inversion are computationally analyzed. We demonstrate using synthetic data that the TLSM indicator has the unique ability to recover weak (or hard-to-reach) scatterers and has the potential to generate higher quality images compared to LSM. Provided high-SNR measurements, this advantage may be preserved in reconstructions from LU test data.

Ensemble WSINDy for Data Driven Discovery of Governing Equations from Laser-based Full-field Measurements

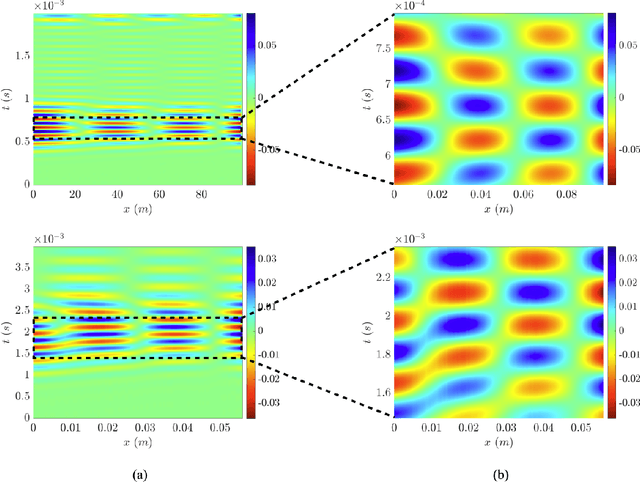
This work leverages laser vibrometry and the weak form of the sparse identification of nonlinear dynamics (WSINDy) for partial differential equations to learn macroscale governing equations from full-field experimental data. In the experiments, two beam-like specimens, one aluminum and one IDOX/Estane composite, are subjected to shear wave excitation in the low frequency regime and the response is measured in the form of particle velocity on the specimen surface. The WSINDy for PDEs algorithm is applied to the resulting spatio-temporal data to discover the effective dynamics of the specimens from a family of potential PDEs. The discovered PDE is of the recognizable Euler-Bernoulli beam model form, from which the Young's modulus for the two materials are estimated. An ensemble version of the WSINDy algorithm is also used which results in information about the uncertainty in the PDE coefficients and Young's moduli. The discovered PDEs are also simulated with a finite element code to compare against the experimental data with reasonable accuracy. Using full-field experimental data and WSINDy together is a powerful non-destructive approach for learning unknown governing equations and gaining insights about mechanical systems in the dynamic regime.

Deep learning for full-field ultrasonic characterization

This study takes advantage of recent advances in machine learning to establish a physics-based data analytic platform for distributed reconstruction of mechanical properties in layered components from full waveform data. In this vein, two logics, namely the direct inversion and physics-informed neural networks (PINNs), are explored. The direct inversion entails three steps: (i) spectral denoising and differentiation of the full-field data, (ii) building appropriate neural maps to approximate the profile of unknown physical and regularization parameters on their respective domains, and (iii) simultaneous training of the neural networks by minimizing the Tikhonov-regularized PDE loss using data from (i). PINNs furnish efficient surrogate models of complex systems with predictive capabilities via multitask learning where the field variables are modeled by neural maps endowed with (scaler or distributed) auxiliary parameters such as physical unknowns and loss function weights. PINNs are then trained by minimizing a measure of data misfit subject to the underlying physical laws as constraints. In this study, to facilitate learning from ultrasonic data, the PINNs loss adopts (a) wavenumber-dependent Sobolev norms to compute the data misfit, and (b) non-adaptive weights in a specific scaling framework to naturally balance the loss objectives by leveraging the form of PDEs germane to elastic-wave propagation. Both paradigms are examined via synthetic and laboratory test data. In the latter case, the reconstructions are performed at multiple frequencies and the results are verified by a set of complementary experiments highlighting the importance of verification and validation in data-driven modeling.