DARE the Extreme: Revisiting Delta-Parameter Pruning For Fine-Tuned Models

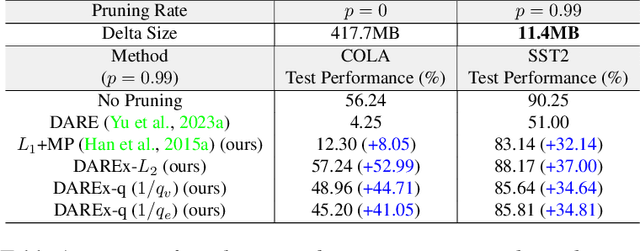
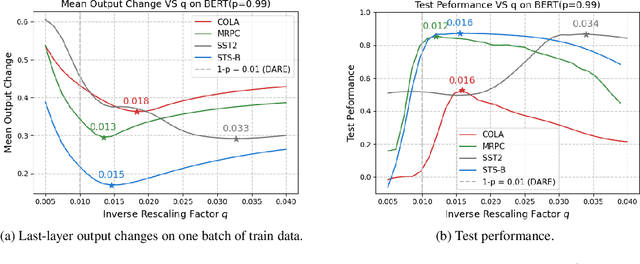
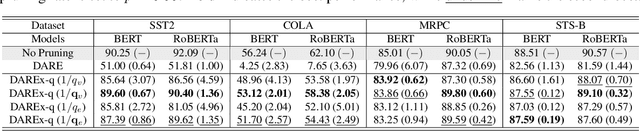
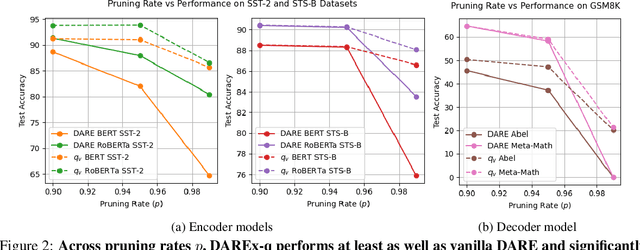
Storing open-source fine-tuned models separately introduces redundancy and increases response times in applications utilizing multiple models. Delta-parameter pruning (DPP), particularly the random drop and rescale (DARE) method proposed by Yu et al., addresses this by pruning the majority of delta parameters--the differences between fine-tuned and pre-trained model weights--while typically maintaining minimal performance loss. However, DARE fails when either the pruning rate or the magnitude of the delta parameters is large. We highlight two key reasons for this failure: (1) an excessively large rescaling factor as pruning rates increase, and (2) high mean and variance in the delta parameters. To push DARE's limits, we introduce DAREx (DARE the eXtreme), which features two algorithmic improvements: (1) DAREx-q, a rescaling factor modification that significantly boosts performance at high pruning rates (e.g., >30 % on COLA and SST2 for encoder models, with even greater gains in decoder models), and (2) DAREx-L2, which combines DARE with AdamR, an in-training method that applies appropriate delta regularization before DPP. We also demonstrate that DAREx-q can be seamlessly combined with vanilla parameter-efficient fine-tuning techniques like LoRA and can facilitate structural DPP. Additionally, we revisit the application of importance-based pruning techniques within DPP, demonstrating that they outperform random-based methods when delta parameters are large. Through this comprehensive study, we develop a pipeline for selecting the most appropriate DPP method under various practical scenarios.

Implicit Geometry of Next-token Prediction: From Language Sparsity Patterns to Model Representations

Next-token prediction (NTP) over large text corpora has become the go-to paradigm to train large language models. Yet, it remains unclear how NTP influences the mapping of linguistic patterns to geometric properties of the resulting model representations. We frame training of large language models as soft-label classification over sparse probabilistic label vectors, coupled with an analytical approximation that allows unrestricted generation of context embeddings. This approach links NTP training to rank-constrained, nuclear-norm regularized optimization in the logit domain, offering a framework for analyzing the geometry of word and context embeddings. In large embedding spaces, we find that NTP implicitly favors learning logits with a sparse plus low-rank structure. While the sparse component captures the co-occurrence frequency of context-word pairs, the orthogonal low-rank component, which becomes dominant as training progresses, depends solely on the sparsity pattern of the co-occurrence matrix. Consequently, when projected onto an appropriate subspace, representations of contexts that are followed by the same set of next-tokens collapse, a phenomenon we term subspace-collapse. We validate our findings on synthetic and small-scale real language datasets. Finally, we outline potential research directions aimed at deepening the understanding of NTP's influence on the learning of linguistic patterns and regularities.

Engineering the Neural Collapse Geometry of Supervised-Contrastive Loss

Supervised-contrastive loss (SCL) is an alternative to cross-entropy (CE) for classification tasks that makes use of similarities in the embedding space to allow for richer representations. In this work, we propose methods to engineer the geometry of these learnt feature embeddings by modifying the contrastive loss. In pursuit of adjusting the geometry we explore the impact of prototypes, fixed embeddings included during training to alter the final feature geometry. Specifically, through empirical findings, we demonstrate that the inclusion of prototypes in every batch induces the geometry of the learnt embeddings to align with that of the prototypes. We gain further insights by considering a limiting scenario where the number of prototypes far outnumber the original batch size. Through this, we establish a connection to cross-entropy (CE) loss with a fixed classifier and normalized embeddings. We validate our findings by conducting a series of experiments with deep neural networks on benchmark vision datasets.

Supervised-Contrastive Loss Learns Orthogonal Frames and Batching Matters

Supervised contrastive loss (SCL) is a competitive and often superior alternative to the cross-entropy (CE) loss for classification. In this paper we ask: what differences in the learning process occur when the two different loss functions are being optimized? To answer this question, our main finding is that the geometry of embeddings learned by SCL forms an orthogonal frame (OF) regardless of the number of training examples per class. This is in contrast to the CE loss, for which previous work has shown that it learns embeddings geometries that are highly dependent on the class sizes. We arrive at our finding theoretically, by proving that the global minimizers of an unconstrained features model with SCL loss and entry-wise non-negativity constraints form an OF. We then validate the model's prediction by conducting experiments with standard deep-learning models on benchmark vision datasets. Finally, our analysis and experiments reveal that the batching scheme chosen during SCL training plays a critical role in determining the quality of convergence to the OF geometry. This finding motivates a simple algorithm wherein the addition of a few binding examples in each batch significantly speeds up the occurrence of the OF geometry.

On the Implicit Geometry of Cross-Entropy Parameterizations for Label-Imbalanced Data

Various logit-adjusted parameterizations of the cross-entropy (CE) loss have been proposed as alternatives to weighted CE for training large models on label-imbalanced data far beyond the zero train error regime. The driving force behind those designs has been the theory of implicit bias, which for linear(ized) models, explains why they successfully induce bias on the optimization path towards solutions that favor minorities. Aiming to extend this theory to non-linear models, we investigate the implicit geometry of classifiers and embeddings that are learned by different CE parameterizations. Our main result characterizes the global minimizers of a non-convex cost-sensitive SVM classifier for the unconstrained features model, which serves as an abstraction of deep nets. We derive closed-form formulas for the angles and norms of classifiers and embeddings as a function of the number of classes, the imbalance and the minority ratios, and the loss hyperparameters. Using these, we show that logit-adjusted parameterizations can be appropriately tuned to learn symmetric geometries irrespective of the imbalance ratio. We complement our analysis with experiments and an empirical study of convergence accuracy in deep-nets.

Imbalance Trouble: Revisiting Neural-Collapse Geometry

Neural Collapse refers to the remarkable structural properties characterizing the geometry of class embeddings and classifier weights, found by deep nets when trained beyond zero training error. However, this characterization only holds for balanced data. Here we thus ask whether it can be made invariant to class imbalances. Towards this end, we adopt the unconstrained-features model (UFM), a recent theoretical model for studying neural collapse, and introduce Simplex-Encoded-Labels Interpolation (SELI) as an invariant characterization of the neural collapse phenomenon. Specifically, we prove for the UFM with cross-entropy loss and vanishing regularization that, irrespective of class imbalances, the embeddings and classifiers always interpolate a simplex-encoded label matrix and that their individual geometries are determined by the SVD factors of this same label matrix. We then present extensive experiments on synthetic and real datasets that confirm convergence to the SELI geometry. However, we caution that convergence worsens with increasing imbalances. We theoretically support this finding by showing that unlike the balanced case, when minorities are present, ridge-regularization plays a critical role in tweaking the geometry. This defines new questions and motivates further investigations into the impact of class imbalances on the rates at which first-order methods converge to their asymptotically preferred solutions.