Imbalance Trouble: Revisiting Neural-Collapse Geometry
Paper and Code
Aug 10, 2022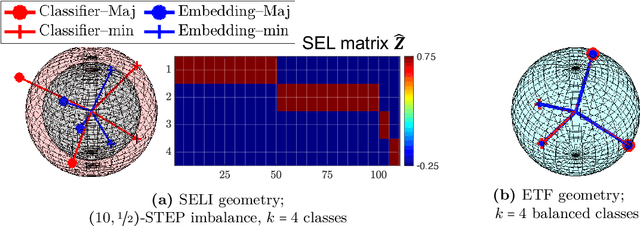

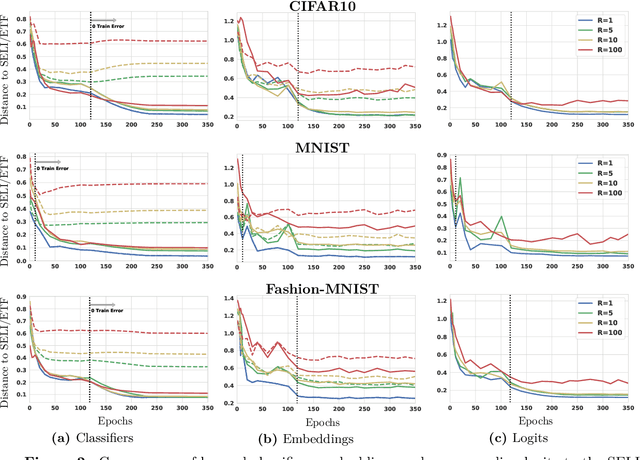
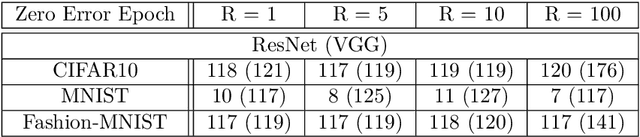
Neural Collapse refers to the remarkable structural properties characterizing the geometry of class embeddings and classifier weights, found by deep nets when trained beyond zero training error. However, this characterization only holds for balanced data. Here we thus ask whether it can be made invariant to class imbalances. Towards this end, we adopt the unconstrained-features model (UFM), a recent theoretical model for studying neural collapse, and introduce Simplex-Encoded-Labels Interpolation (SELI) as an invariant characterization of the neural collapse phenomenon. Specifically, we prove for the UFM with cross-entropy loss and vanishing regularization that, irrespective of class imbalances, the embeddings and classifiers always interpolate a simplex-encoded label matrix and that their individual geometries are determined by the SVD factors of this same label matrix. We then present extensive experiments on synthetic and real datasets that confirm convergence to the SELI geometry. However, we caution that convergence worsens with increasing imbalances. We theoretically support this finding by showing that unlike the balanced case, when minorities are present, ridge-regularization plays a critical role in tweaking the geometry. This defines new questions and motivates further investigations into the impact of class imbalances on the rates at which first-order methods converge to their asymptotically preferred solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge