Deep Learning-Based Correction and Unmixing of Hyperspectral Images for Brain Tumor Surgery

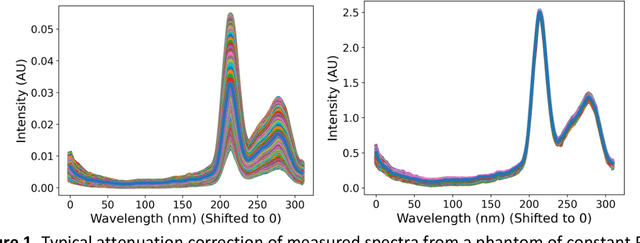
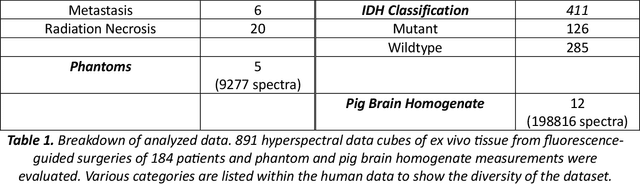
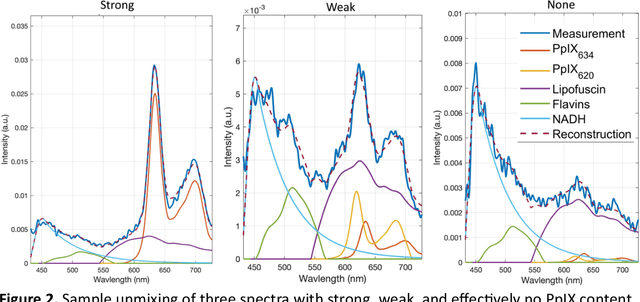
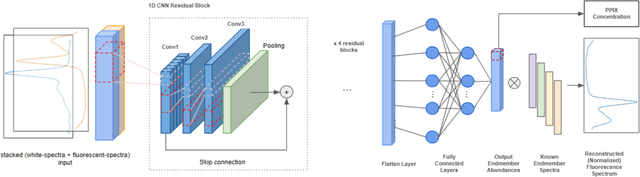
Hyperspectral Imaging (HSI) for fluorescence-guided brain tumor resection enables visualization of differences between tissues that are not distinguishable to humans. This augmentation can maximize brain tumor resection, improving patient outcomes. However, much of the processing in HSI uses simplified linear methods that are unable to capture the non-linear, wavelength-dependent phenomena that must be modeled for accurate recovery of fluorophore abundances. We therefore propose two deep learning models for correction and unmixing, which can account for the nonlinear effects and produce more accurate estimates of abundances. Both models use an autoencoder-like architecture to process the captured spectra. One is trained with protoporphyrin IX (PpIX) concentration labels. The other undergoes semi-supervised training, first learning hyperspectral unmixing self-supervised and then learning to correct fluorescence emission spectra for heterogeneous optical and geometric properties using a reference white-light reflectance spectrum in a few-shot manner. The models were evaluated against phantom and pig brain data with known PpIX concentration; the supervised model achieved Pearson correlation coefficients (R values) between the known and computed PpIX concentrations of 0.997 and 0.990, respectively, whereas the classical approach achieved only 0.93 and 0.82. The semi-supervised approach's R values were 0.98 and 0.91, respectively. On human data, the semi-supervised model gives qualitatively more realistic results than the classical method, better removing bright spots of specular reflectance and reducing the variance in PpIX abundance over biopsies that should be relatively homogeneous. These results show promise for using deep learning to improve HSI in fluorescence-guided neurosurgery.

Engineering the Neural Collapse Geometry of Supervised-Contrastive Loss

Supervised-contrastive loss (SCL) is an alternative to cross-entropy (CE) for classification tasks that makes use of similarities in the embedding space to allow for richer representations. In this work, we propose methods to engineer the geometry of these learnt feature embeddings by modifying the contrastive loss. In pursuit of adjusting the geometry we explore the impact of prototypes, fixed embeddings included during training to alter the final feature geometry. Specifically, through empirical findings, we demonstrate that the inclusion of prototypes in every batch induces the geometry of the learnt embeddings to align with that of the prototypes. We gain further insights by considering a limiting scenario where the number of prototypes far outnumber the original batch size. Through this, we establish a connection to cross-entropy (CE) loss with a fixed classifier and normalized embeddings. We validate our findings by conducting a series of experiments with deep neural networks on benchmark vision datasets.

Supervised-Contrastive Loss Learns Orthogonal Frames and Batching Matters

Supervised contrastive loss (SCL) is a competitive and often superior alternative to the cross-entropy (CE) loss for classification. In this paper we ask: what differences in the learning process occur when the two different loss functions are being optimized? To answer this question, our main finding is that the geometry of embeddings learned by SCL forms an orthogonal frame (OF) regardless of the number of training examples per class. This is in contrast to the CE loss, for which previous work has shown that it learns embeddings geometries that are highly dependent on the class sizes. We arrive at our finding theoretically, by proving that the global minimizers of an unconstrained features model with SCL loss and entry-wise non-negativity constraints form an OF. We then validate the model's prediction by conducting experiments with standard deep-learning models on benchmark vision datasets. Finally, our analysis and experiments reveal that the batching scheme chosen during SCL training plays a critical role in determining the quality of convergence to the OF geometry. This finding motivates a simple algorithm wherein the addition of a few binding examples in each batch significantly speeds up the occurrence of the OF geometry.