Deep Learning-Based Correction and Unmixing of Hyperspectral Images for Brain Tumor Surgery

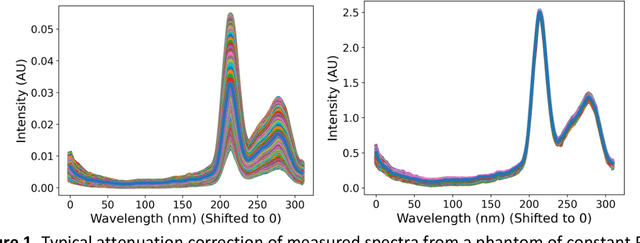
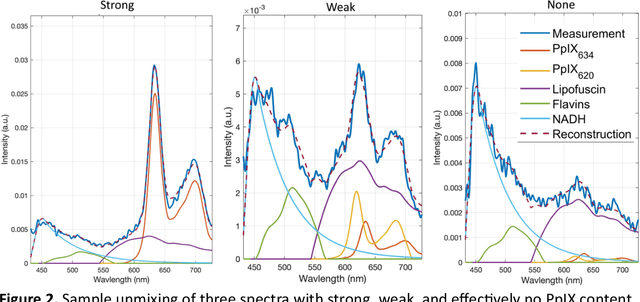
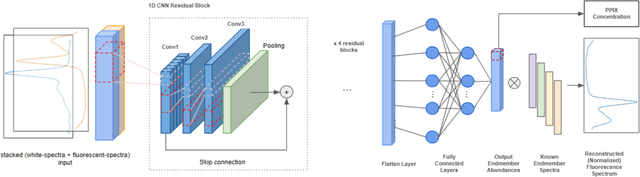
Hyperspectral Imaging (HSI) for fluorescence-guided brain tumor resection enables visualization of differences between tissues that are not distinguishable to humans. This augmentation can maximize brain tumor resection, improving patient outcomes. However, much of the processing in HSI uses simplified linear methods that are unable to capture the non-linear, wavelength-dependent phenomena that must be modeled for accurate recovery of fluorophore abundances. We therefore propose two deep learning models for correction and unmixing, which can account for the nonlinear effects and produce more accurate estimates of abundances. Both models use an autoencoder-like architecture to process the captured spectra. One is trained with protoporphyrin IX (PpIX) concentration labels. The other undergoes semi-supervised training, first learning hyperspectral unmixing self-supervised and then learning to correct fluorescence emission spectra for heterogeneous optical and geometric properties using a reference white-light reflectance spectrum in a few-shot manner. The models were evaluated against phantom and pig brain data with known PpIX concentration; the supervised model achieved Pearson correlation coefficients (R values) between the known and computed PpIX concentrations of 0.997 and 0.990, respectively, whereas the classical approach achieved only 0.93 and 0.82. The semi-supervised approach's R values were 0.98 and 0.91, respectively. On human data, the semi-supervised model gives qualitatively more realistic results than the classical method, better removing bright spots of specular reflectance and reducing the variance in PpIX abundance over biopsies that should be relatively homogeneous. These results show promise for using deep learning to improve HSI in fluorescence-guided neurosurgery.

A Spectral Library and Method for Sparse Unmixing of Hyperspectral Images in Fluorescence Guided Resection of Brain Tumors

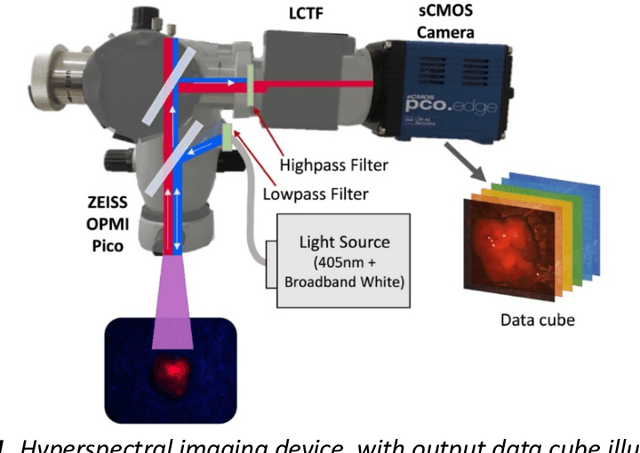
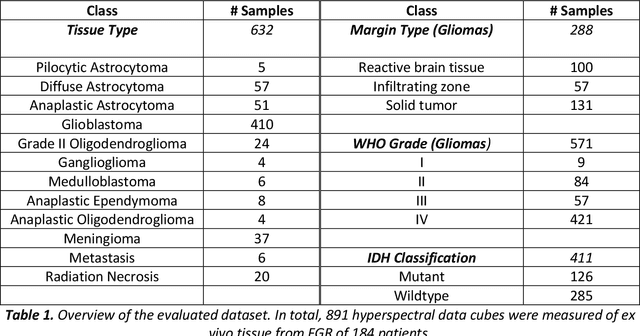
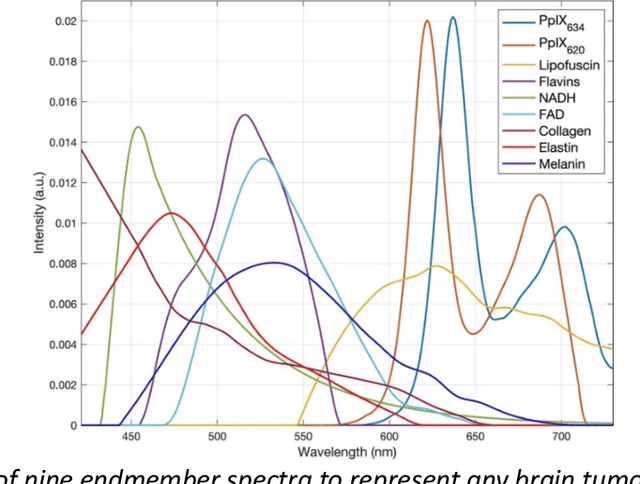
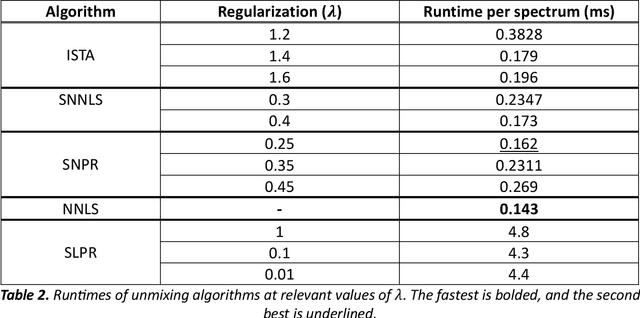
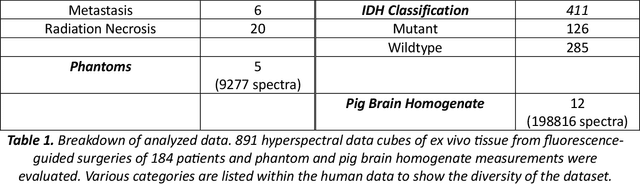
Through spectral unmixing, hyperspectral imaging (HSI) in fluorescence-guided brain tumor surgery has enabled detection and classification of tumor regions invisible to the human eye. Prior unmixing work has focused on determining a minimal set of viable fluorophore spectra known to be present in the brain and effectively reconstructing human data without overfitting. With these endmembers, non-negative least squares regression (NNLS) was used to compute the abundances. However, HSI images are heterogeneous, so one small set of endmember spectra may not fit all pixels well. Additionally, NNLS is the maximum likelihood estimator only if the measurement is normally distributed, and it does not enforce sparsity, which leads to overfitting and unphysical results. Here, we analyzed 555666 HSI fluorescence spectra from 891 ex vivo measurements of patients with brain tumors to show that a Poisson distribution models the measured data 82% better than a Gaussian in terms of the Kullback-Leibler divergence and that the endmember abundance vectors are sparse. With this knowledge, we introduce (1) a library of 9 endmember spectra, (2) a sparse, non-negative Poisson regression algorithm to perform physics-informed unmixing with this library without overfitting, and (3) a highly realistic spectral measurement simulation with known endmember abundances. The new unmixing method was then tested on the human and simulated data and compared to four other candidate methods. It outperforms previous methods with 25% lower error in the computed abundances on the simulated data than NNLS, lower reconstruction error on human data, beUer sparsity, and 31 times faster runtime than state-of-the-art Poisson regression. This method and library of endmember spectra can enable more accurate spectral unmixing to beUer aid the surgeon during brain tumor resection.

A Unified Parallel Algorithm for Regularized Group PLS Scalable to Big Data

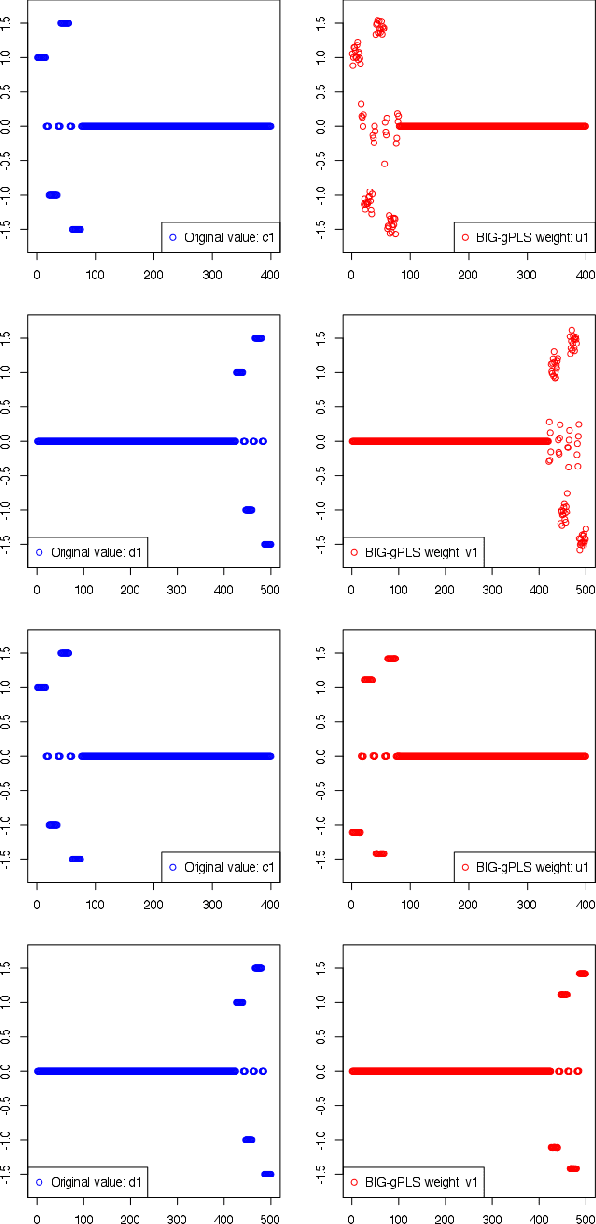
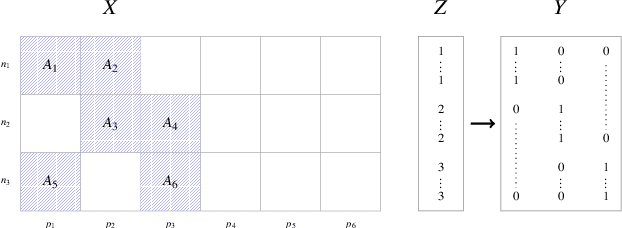
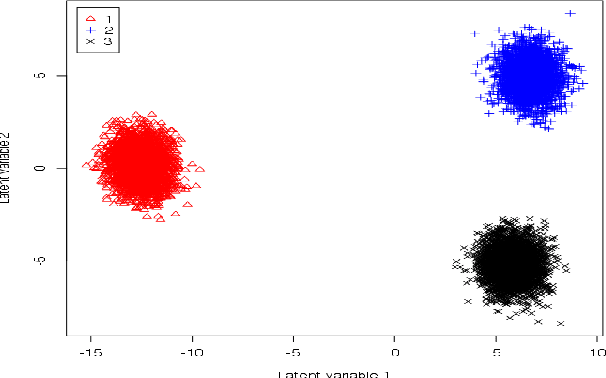
Partial Least Squares (PLS) methods have been heavily exploited to analyse the association between two blocs of data. These powerful approaches can be applied to data sets where the number of variables is greater than the number of observations and in presence of high collinearity between variables. Different sparse versions of PLS have been developed to integrate multiple data sets while simultaneously selecting the contributing variables. Sparse modelling is a key factor in obtaining better estimators and identifying associations between multiple data sets. The cornerstone of the sparsity version of PLS methods is the link between the SVD of a matrix (constructed from deflated versions of the original matrices of data) and least squares minimisation in linear regression. We present here an accurate description of the most popular PLS methods, alongside their mathematical proofs. A unified algorithm is proposed to perform all four types of PLS including their regularised versions. Various approaches to decrease the computation time are offered, and we show how the whole procedure can be scalable to big data sets.