A Spectral Library and Method for Sparse Unmixing of Hyperspectral Images in Fluorescence Guided Resection of Brain Tumors
Paper and Code
Jan 30, 2024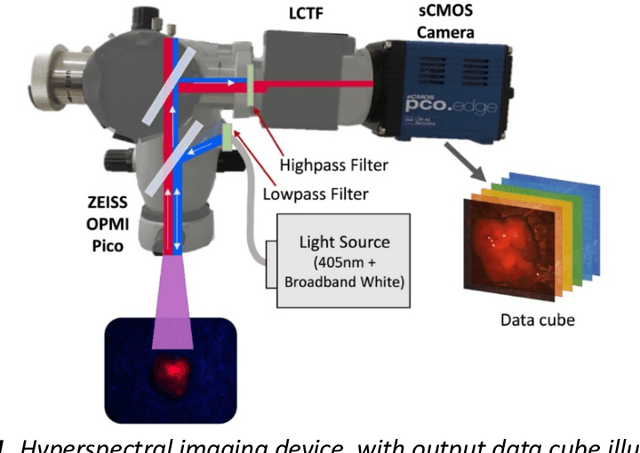
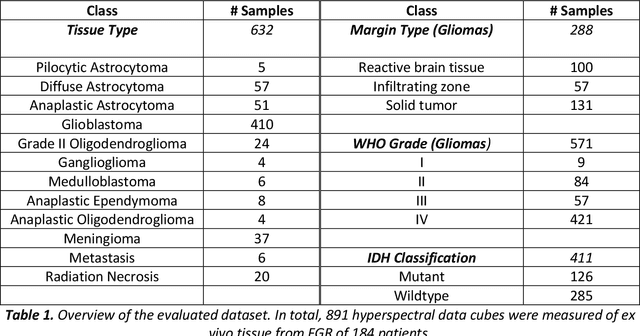
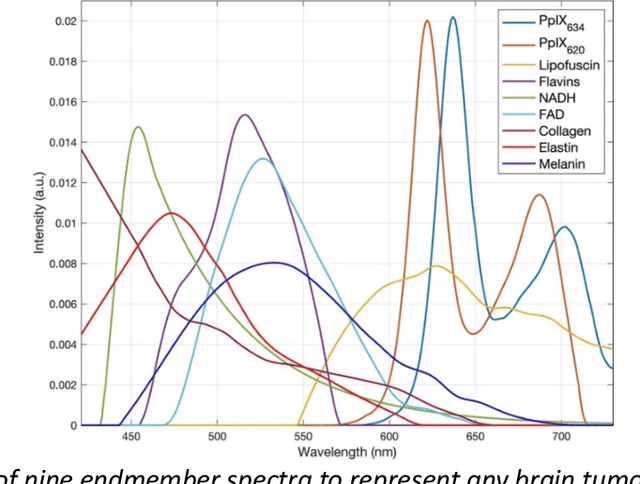
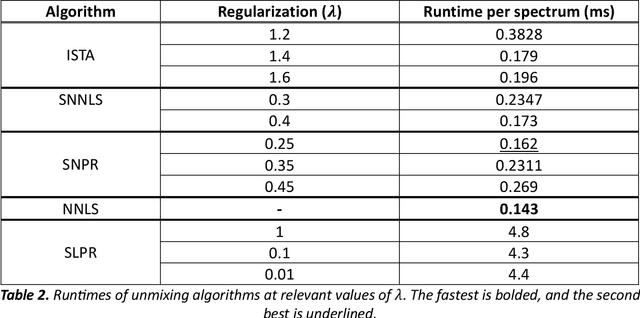
Through spectral unmixing, hyperspectral imaging (HSI) in fluorescence-guided brain tumor surgery has enabled detection and classification of tumor regions invisible to the human eye. Prior unmixing work has focused on determining a minimal set of viable fluorophore spectra known to be present in the brain and effectively reconstructing human data without overfitting. With these endmembers, non-negative least squares regression (NNLS) was used to compute the abundances. However, HSI images are heterogeneous, so one small set of endmember spectra may not fit all pixels well. Additionally, NNLS is the maximum likelihood estimator only if the measurement is normally distributed, and it does not enforce sparsity, which leads to overfitting and unphysical results. Here, we analyzed 555666 HSI fluorescence spectra from 891 ex vivo measurements of patients with brain tumors to show that a Poisson distribution models the measured data 82% better than a Gaussian in terms of the Kullback-Leibler divergence and that the endmember abundance vectors are sparse. With this knowledge, we introduce (1) a library of 9 endmember spectra, (2) a sparse, non-negative Poisson regression algorithm to perform physics-informed unmixing with this library without overfitting, and (3) a highly realistic spectral measurement simulation with known endmember abundances. The new unmixing method was then tested on the human and simulated data and compared to four other candidate methods. It outperforms previous methods with 25% lower error in the computed abundances on the simulated data than NNLS, lower reconstruction error on human data, beUer sparsity, and 31 times faster runtime than state-of-the-art Poisson regression. This method and library of endmember spectra can enable more accurate spectral unmixing to beUer aid the surgeon during brain tumor resection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge