A Machine Learning Framework for Handling Unreliable Absence Label and Class Imbalance for Marine Stinger Beaching Prediction

Bluebottles (\textit{Physalia} spp.) are marine stingers resembling jellyfish, whose presence on Australian beaches poses a significant public risk due to their venomous nature. Understanding the environmental factors driving bluebottles ashore is crucial for mitigating their impact, and machine learning tools are to date relatively unexplored. We use bluebottle marine stinger presence/absence data from beaches in Eastern Sydney, Australia, and compare machine learning models (Multilayer Perceptron, Random Forest, and XGBoost) to identify factors influencing their presence. We address challenges such as class imbalance, class overlap, and unreliable absence data by employing data augmentation techniques, including the Synthetic Minority Oversampling Technique (SMOTE), Random Undersampling, and Synthetic Negative Approach that excludes the negative class. Our results show that SMOTE failed to resolve class overlap, but the presence-focused approach effectively handled imbalance, class overlap, and ambiguous absence data. The data attributes such as the wind direction, which is a circular variable, emerged as a key factor influencing bluebottle presence, confirming previous inference studies. However, in the absence of population dynamics, biological behaviours, and life cycles, the best predictive model appears to be Random Forests combined with Synthetic Negative Approach. This research contributes to mitigating the risks posed by bluebottles to beachgoers and provides insights into handling class overlap and unreliable negative class in environmental modelling.

A Unified Parallel Algorithm for Regularized Group PLS Scalable to Big Data

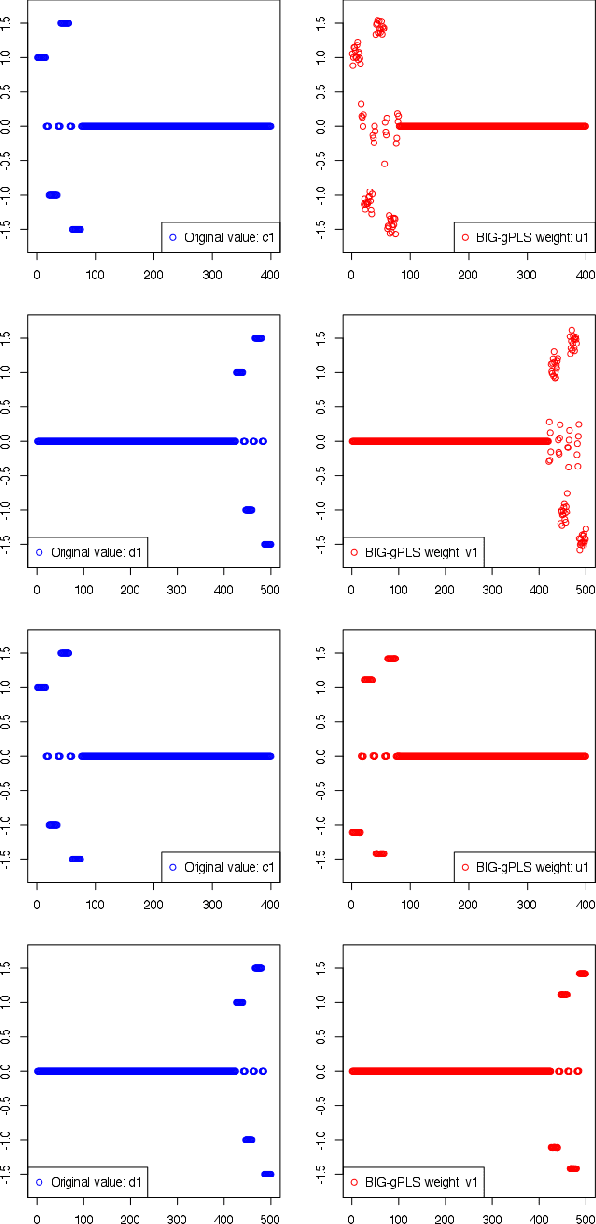
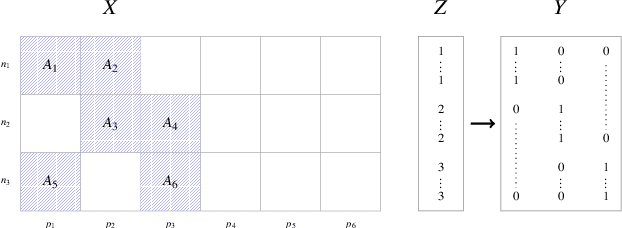
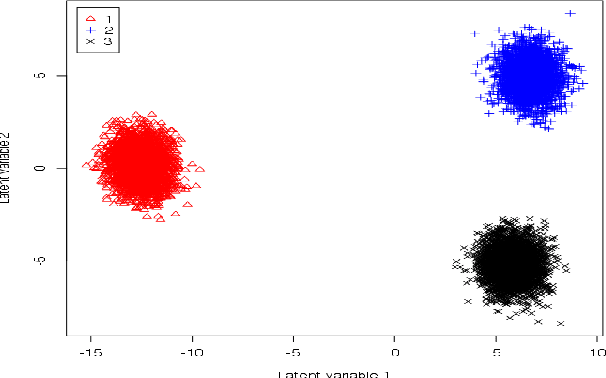
Partial Least Squares (PLS) methods have been heavily exploited to analyse the association between two blocs of data. These powerful approaches can be applied to data sets where the number of variables is greater than the number of observations and in presence of high collinearity between variables. Different sparse versions of PLS have been developed to integrate multiple data sets while simultaneously selecting the contributing variables. Sparse modelling is a key factor in obtaining better estimators and identifying associations between multiple data sets. The cornerstone of the sparsity version of PLS methods is the link between the SVD of a matrix (constructed from deflated versions of the original matrices of data) and least squares minimisation in linear regression. We present here an accurate description of the most popular PLS methods, alongside their mathematical proofs. A unified algorithm is proposed to perform all four types of PLS including their regularised versions. Various approaches to decrease the computation time are offered, and we show how the whole procedure can be scalable to big data sets.