Implicit Geometry of Next-token Prediction: From Language Sparsity Patterns to Model Representations
Paper and Code
Aug 27, 2024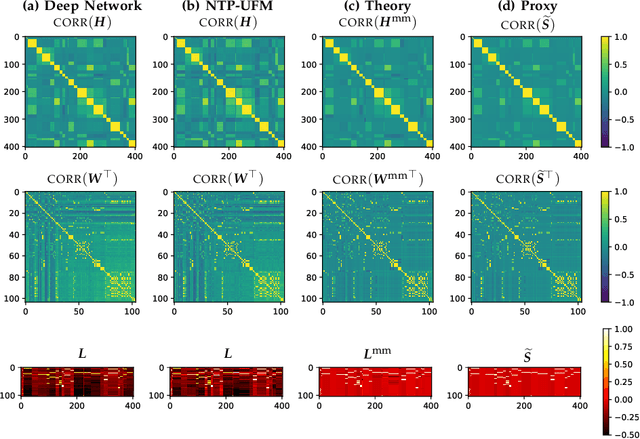
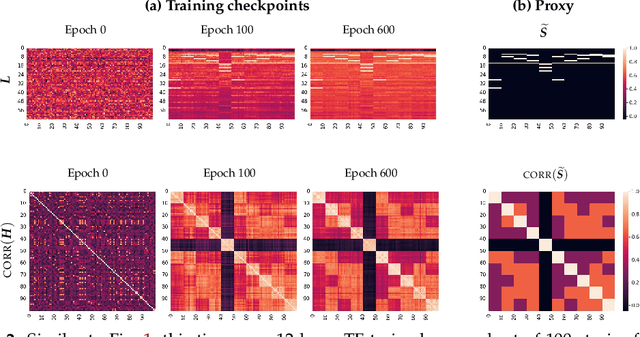
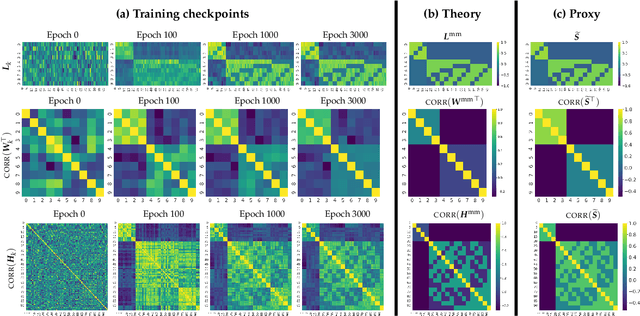

Next-token prediction (NTP) over large text corpora has become the go-to paradigm to train large language models. Yet, it remains unclear how NTP influences the mapping of linguistic patterns to geometric properties of the resulting model representations. We frame training of large language models as soft-label classification over sparse probabilistic label vectors, coupled with an analytical approximation that allows unrestricted generation of context embeddings. This approach links NTP training to rank-constrained, nuclear-norm regularized optimization in the logit domain, offering a framework for analyzing the geometry of word and context embeddings. In large embedding spaces, we find that NTP implicitly favors learning logits with a sparse plus low-rank structure. While the sparse component captures the co-occurrence frequency of context-word pairs, the orthogonal low-rank component, which becomes dominant as training progresses, depends solely on the sparsity pattern of the co-occurrence matrix. Consequently, when projected onto an appropriate subspace, representations of contexts that are followed by the same set of next-tokens collapse, a phenomenon we term subspace-collapse. We validate our findings on synthetic and small-scale real language datasets. Finally, we outline potential research directions aimed at deepening the understanding of NTP's influence on the learning of linguistic patterns and regularities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge