The Rich and the Simple: On the Implicit Bias of Adam and SGD

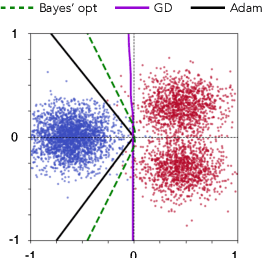
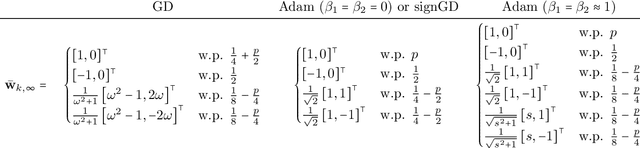
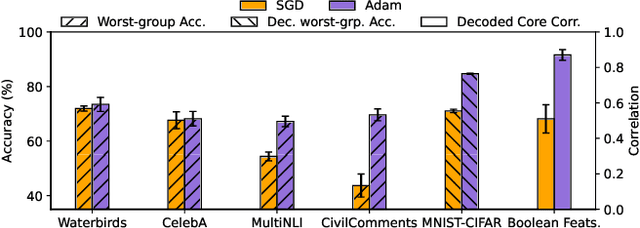
Adam is the de facto optimization algorithm for several deep learning applications, but an understanding of its implicit bias and how it differs from other algorithms, particularly standard first-order methods such as (stochastic) gradient descent (GD), remains limited. In practice, neural networks trained with SGD are known to exhibit simplicity bias -- a tendency to find simple solutions. In contrast, we show that Adam is more resistant to such simplicity bias. To demystify this phenomenon, in this paper, we investigate the differences in the implicit biases of Adam and GD when training two-layer ReLU neural networks on a binary classification task involving synthetic data with Gaussian clusters. We find that GD exhibits a simplicity bias, resulting in a linear decision boundary with a suboptimal margin, whereas Adam leads to much richer and more diverse features, producing a nonlinear boundary that is closer to the Bayes' optimal predictor. This richer decision boundary also allows Adam to achieve higher test accuracy both in-distribution and under certain distribution shifts. We theoretically prove these results by analyzing the population gradients. To corroborate our theoretical findings, we present empirical results showing that this property of Adam leads to superior generalization across datasets with spurious correlations where neural networks trained with SGD are known to show simplicity bias and don't generalize well under certain distributional shifts.

Simplicity Bias of Transformers to Learn Low Sensitivity Functions

Transformers achieve state-of-the-art accuracy and robustness across many tasks, but an understanding of the inductive biases that they have and how those biases are different from other neural network architectures remains elusive. Various neural network architectures such as fully connected networks have been found to have a simplicity bias towards simple functions of the data; one version of this simplicity bias is a spectral bias to learn simple functions in the Fourier space. In this work, we identify the notion of sensitivity of the model to random changes in the input as a notion of simplicity bias which provides a unified metric to explain the simplicity and spectral bias of transformers across different data modalities. We show that transformers have lower sensitivity than alternative architectures, such as LSTMs, MLPs and CNNs, across both vision and language tasks. We also show that low-sensitivity bias correlates with improved robustness; furthermore, it can also be used as an efficient intervention to further improve the robustness of transformers.

Implicit Bias and Fast Convergence Rates for Self-attention

Self-attention, the core mechanism of transformers, distinguishes them from traditional neural networks and drives their outstanding performance. Towards developing the fundamental optimization principles of self-attention, we investigate the implicit bias of gradient descent (GD) in training a self-attention layer with fixed linear decoder in binary classification. Drawing inspiration from the study of GD in linear logistic regression over separable data, recent work demonstrates that as the number of iterations $t$ approaches infinity, the key-query matrix $W_t$ converges locally (with respect to the initialization direction) to a hard-margin SVM solution $W_{mm}$. Our work enhances this result in four aspects. Firstly, we identify non-trivial data settings for which convergence is provably global, thus shedding light on the optimization landscape. Secondly, we provide the first finite-time convergence rate for $W_t$ to $W_{mm}$, along with quantifying the rate of sparsification in the attention map. Thirdly, through an analysis of normalized GD and Polyak step-size, we demonstrate analytically that adaptive step-size rules can accelerate the convergence of self-attention. Additionally, we remove the restriction of prior work on a fixed linear decoder. Our results reinforce the implicit-bias perspective of self-attention and strengthen its connections to implicit-bias in linear logistic regression, despite the intricate non-convex nature of the former.

Mitigating Simplicity Bias in Deep Learning for Improved OOD Generalization and Robustness

Neural networks (NNs) are known to exhibit simplicity bias where they tend to prefer learning 'simple' features over more 'complex' ones, even when the latter may be more informative. Simplicity bias can lead to the model making biased predictions which have poor out-of-distribution (OOD) generalization. To address this, we propose a framework that encourages the model to use a more diverse set of features to make predictions. We first train a simple model, and then regularize the conditional mutual information with respect to it to obtain the final model. We demonstrate the effectiveness of this framework in various problem settings and real-world applications, showing that it effectively addresses simplicity bias and leads to more features being used, enhances OOD generalization, and improves subgroup robustness and fairness. We complement these results with theoretical analyses of the effect of the regularization and its OOD generalization properties.

LoOp: Looking for Optimal Hard Negative Embeddings for Deep Metric Learning

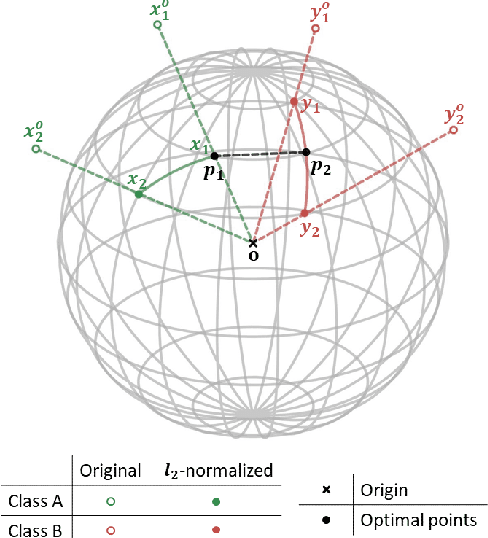
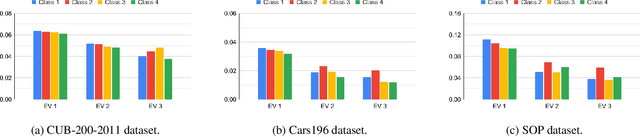
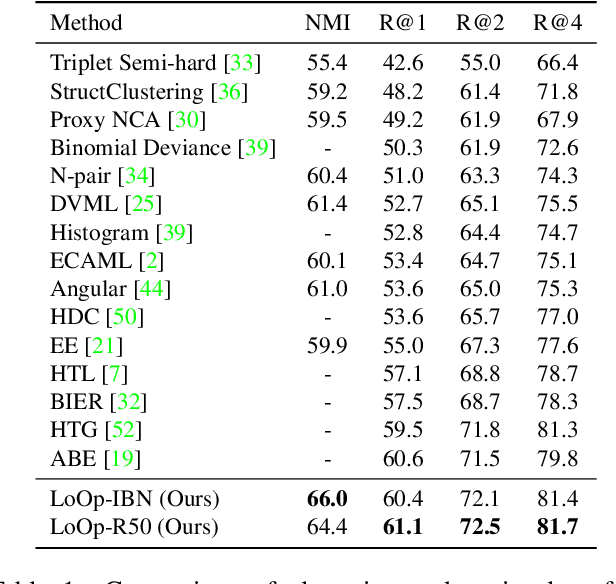
Deep metric learning has been effectively used to learn distance metrics for different visual tasks like image retrieval, clustering, etc. In order to aid the training process, existing methods either use a hard mining strategy to extract the most informative samples or seek to generate hard synthetics using an additional network. Such approaches face different challenges and can lead to biased embeddings in the former case, and (i) harder optimization (ii) slower training speed (iii) higher model complexity in the latter case. In order to overcome these challenges, we propose a novel approach that looks for optimal hard negatives (LoOp) in the embedding space, taking full advantage of each tuple by calculating the minimum distance between a pair of positives and a pair of negatives. Unlike mining-based methods, our approach considers the entire space between pairs of embeddings to calculate the optimal hard negatives. Extensive experiments combining our approach and representative metric learning losses reveal a significant boost in performance on three benchmark datasets.

Multi-Phase Locking Value: A Generalized Method for Determining Instantaneous Multi-frequency Phase Coupling

Many physical, biological and neural systems behave as coupled oscillators, with characteristic phase coupling across different frequencies. Methods such as $n:m$ phase locking value and bi-phase locking value have previously been proposed to quantify phase coupling between two resonant frequencies (e.g. $f$, $2f/3$) and across three frequencies (e.g. $f_1$, $f_2$, $f_1+f_2$), respectively. However, the existing phase coupling metrics have their limitations and limited applications. They cannot be used to detect or quantify phase coupling across multiple frequencies (e.g. $f_1$, $f_2$, $f_3$, $f_4$, $f_1+f_2+f_3-f_4$), or coupling that involves non-integer multiples of the frequencies (e.g. $f_1$, $f_2$, $2f_1/3+f_2/3$). To address the gap, this paper proposes a generalized approach, named multi-phase locking value (M-PLV), for the quantification of various types of instantaneous multi-frequency phase coupling. Different from most instantaneous phase coupling metrics that measure the simultaneous phase coupling, the proposed M-PLV method also allows the detection of delayed phase coupling and the associated time lag between coupled oscillators. The M-PLV has been tested on cases where synthetic coupled signals are generated using white Gaussian signals, and a system comprised of multiple coupled R\"ossler oscillators. Results indicate that the M-PLV can provide a reliable estimation of the time window and frequency combination where the phase coupling is significant, as well as a precise determination of time lag in the case of delayed coupling. This method has the potential to become a powerful new tool for exploring phase coupling in complex nonlinear dynamic systems.

AIM 2020 Challenge on Learned Image Signal Processing Pipeline

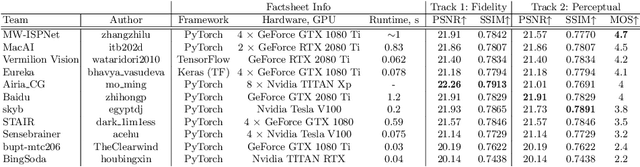
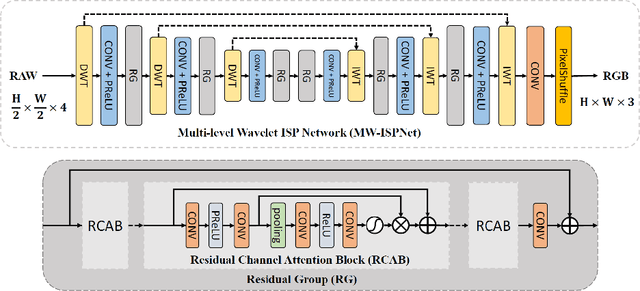
This paper reviews the second AIM learned ISP challenge and provides the description of the proposed solutions and results. The participating teams were solving a real-world RAW-to-RGB mapping problem, where to goal was to map the original low-quality RAW images captured by the Huawei P20 device to the same photos obtained with the Canon 5D DSLR camera. The considered task embraced a number of complex computer vision subtasks, such as image demosaicing, denoising, white balancing, color and contrast correction, demoireing, etc. The target metric used in this challenge combined fidelity scores (PSNR and SSIM) with solutions' perceptual results measured in a user study. The proposed solutions significantly improved the baseline results, defining the state-of-the-art for practical image signal processing pipeline modeling.

Co-VeGAN: Complex-Valued Generative Adversarial Network for Compressive Sensing MR Image Reconstruction

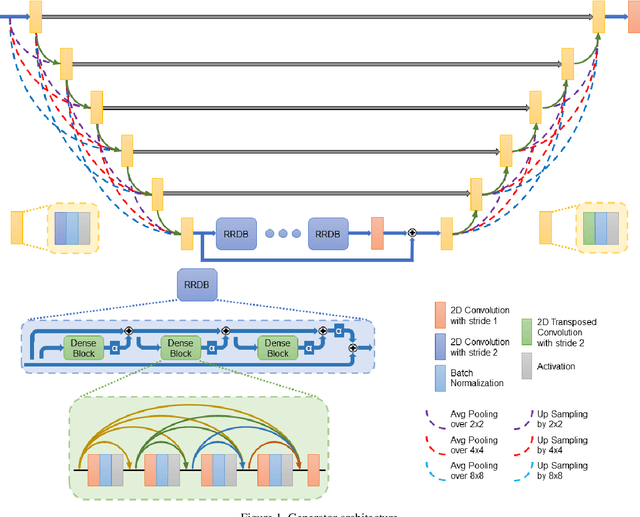
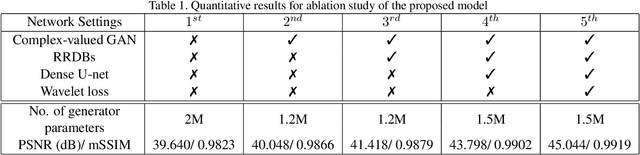
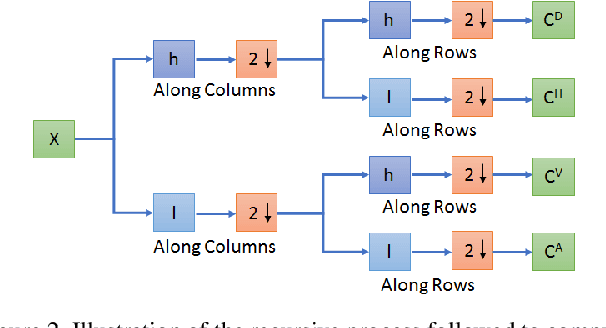
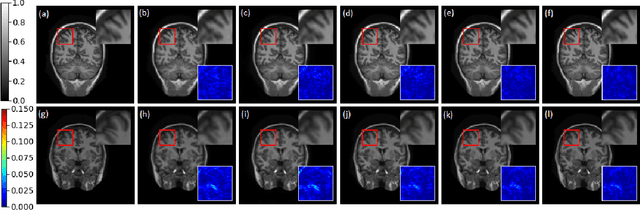
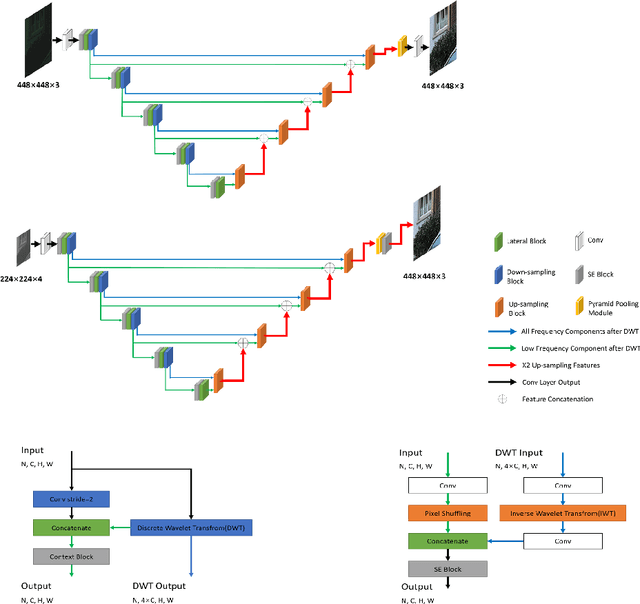
Compressive sensing (CS) is widely used to reduce the image acquisition time of magnetic resonance imaging (MRI). Though CS based undersampling has numerous benefits, like high quality images with less motion artefacts, low storage requirement, etc., the reconstruction of the image from the CS-undersampled data is an ill-posed inverse problem which requires extensive computation and resources. In this paper, we propose a novel deep network that can process complex-valued input to perform high-quality reconstruction. Our model is based on generative adversarial network (GAN) that uses residual-in-residual dense blocks in a modified U-net generator with patch based discriminator. We introduce a wavelet based loss in the complex GAN model for better reconstruction quality. Extensive analyses on different datasets demonstrate that the proposed model significantly outperforms the existing CS reconstruction techniques in terms of peak signal-to-noise ratio and structural similarity index.

Robust Compressive Sensing MRI Reconstruction using Generative Adversarial Networks

Compressive sensing magnetic resonance imaging (CS-MRI) accelerates the acquisition of MR images by breaking the Nyquist sampling limit. In this work, a novel generative adversarial network (GAN) based framework for CS-MRI reconstruction is proposed. Leveraging a combination of patchGAN discriminator and structural similarity index based loss, our model focuses on preserving high frequency content as well as fine textural details in the reconstructed image. Dense and residual connections have been incorporated in a U-net based generator architecture to allow easier transfer of information as well as variable network length. We show that our algorithm outperforms state-of-the-art methods in terms of quality of reconstruction and robustness to noise. Also, the reconstruction time, which is of the order of milliseconds, makes it highly suitable for real-time clinical use.