Differentially Private Latent Diffusion Models

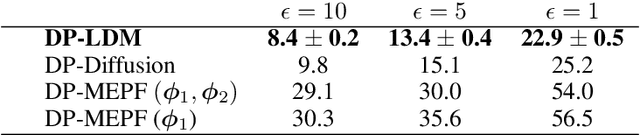
Diffusion models (DMs) are widely used for generating high-quality image datasets. However, since they operate directly in the high-dimensional pixel space, optimization of DMs is computationally expensive, requiring long training times. This contributes to large amounts of noise being injected into the differentially private learning process, due to the composability property of differential privacy. To address this challenge, we propose training Latent Diffusion Models (LDMs) with differential privacy. LDMs use powerful pre-trained autoencoders to reduce the high-dimensional pixel space to a much lower-dimensional latent space, making training DMs more efficient and fast. Unlike [Ghalebikesabi et al., 2023] that pre-trains DMs with public data then fine-tunes them with private data, we fine-tune only the attention modules of LDMs at varying layers with privacy-sensitive data, reducing the number of trainable parameters by approximately 96% compared to fine-tuning the entire DM. We test our algorithm on several public-private data pairs, such as ImageNet as public data and CIFAR10 and CelebA as private data, and SVHN as public data and MNIST as private data. Our approach provides a promising direction for training more powerful, yet training-efficient differentially private DMs that can produce high-quality synthetic images.

Differentially Private Kernel Inducing Points (DP-KIP) for Privacy-preserving Data Distillation

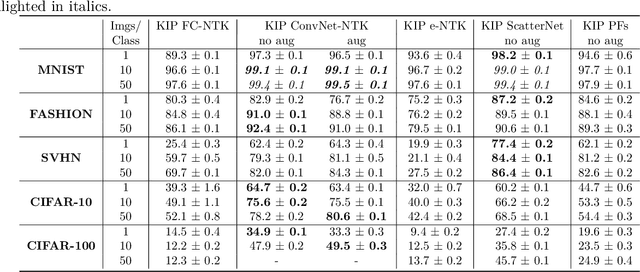
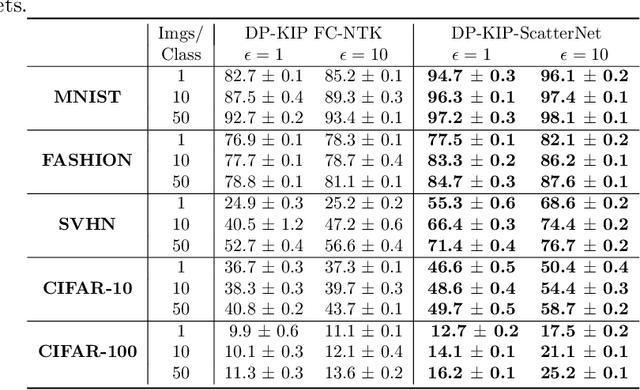
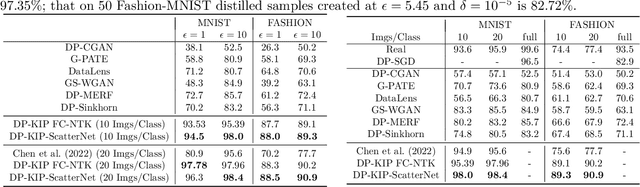
While it is tempting to believe that data distillation preserves privacy, distilled data's empirical robustness against known attacks does not imply a provable privacy guarantee. Here, we develop a provably privacy-preserving data distillation algorithm, called differentially private kernel inducing points (DP-KIP). DP-KIP is an instantiation of DP-SGD on kernel ridge regression (KRR). Following a recent work, we use neural tangent kernels and minimize the KRR loss to estimate the distilled datapoints (i.e., kernel inducing points). We provide a computationally efficient JAX implementation of DP-KIP, which we test on several popular image and tabular datasets to show its efficacy in data distillation with differential privacy guarantees.

DP-SEP! Differentially Private Stochastic Expectation Propagation

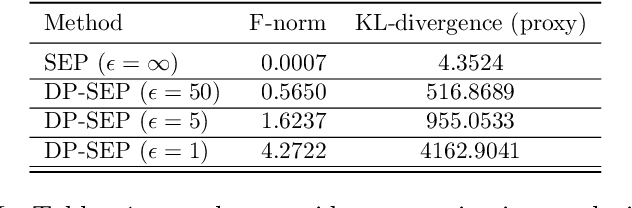
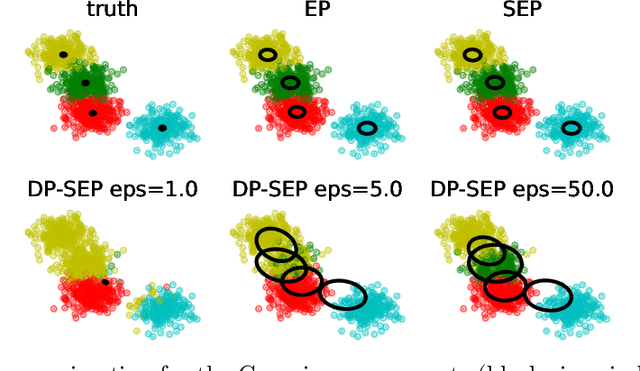
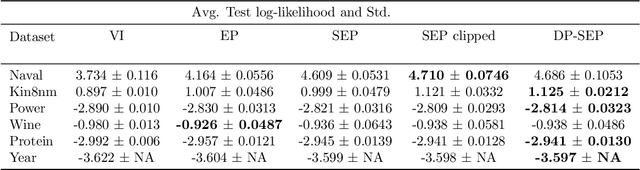
We are interested in privatizing an approximate posterior inference algorithm called Expectation Propagation (EP). EP approximates the posterior by iteratively refining approximations to the local likelihoods, and is known to provide better posterior uncertainties than those by variational inference (VI). However, using EP for large-scale datasets imposes a challenge in terms of memory requirements as it needs to maintain each of the local approximates in memory. To overcome this problem, stochastic expectation propagation (SEP) was proposed, which only considers a unique local factor that captures the average effect of each likelihood term to the posterior and refines it in a way analogous to EP. In terms of privacy, SEP is more tractable than EP because at each refining step of a factor, the remaining factors are fixed to the same value and do not depend on other datapoints as in EP, which makes the sensitivity analysis tractable. We provide a theoretical analysis of the privacy-accuracy trade-off in the posterior estimates under differentially private stochastic expectation propagation (DP-SEP). Furthermore, we demonstrate the performance of our DP-SEP algorithm evaluated on both synthetic and real-world datasets in terms of the quality of posterior estimates at different levels of guaranteed privacy.

Polynomial magic! Hermite polynomials for private data generation

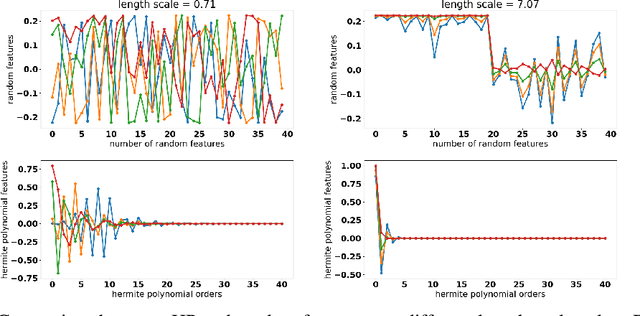
Kernel mean embedding is a useful tool to compare probability measures. Despite its usefulness, kernel mean embedding considers infinite-dimensional features, which are challenging to handle in the context of differentially private data generation. A recent work proposes to approximate the kernel mean embedding of data distribution using finite-dimensional random features, where the sensitivity of the features becomes analytically tractable. More importantly, this approach significantly reduces the privacy cost, compared to other known privatization methods (e.g., DP-SGD), as the approximate kernel mean embedding of the data distribution is privatized only once and can then be repeatedly used during training of a generator without incurring any further privacy cost. However, the required number of random features is excessively high, often ten thousand to a hundred thousand, which worsens the sensitivity of the approximate kernel mean embedding. To improve the sensitivity, we propose to replace random features with Hermite polynomial features. Unlike the random features, the Hermite polynomial features are ordered, where the features at the low orders contain more information on the distribution than those at the high orders. Hence, a relatively low order of Hermite polynomial features can more accurately approximate the mean embedding of the data distribution compared to a significantly higher number of random features. As a result, using the Hermite polynomial features, we significantly improve the privacy-accuracy trade-off, reflected in the high quality and diversity of the generated data, when tested on several heterogeneous tabular datasets, as well as several image benchmark datasets.