A Unifying Post-Processing Framework for Multi-Objective Learn-to-Defer Problems

Learn-to-Defer is a paradigm that enables learning algorithms to work not in isolation but as a team with human experts. In this paradigm, we permit the system to defer a subset of its tasks to the expert. Although there are currently systems that follow this paradigm and are designed to optimize the accuracy of the final human-AI team, the general methodology for developing such systems under a set of constraints (e.g., algorithmic fairness, expert intervention budget, defer of anomaly, etc.) remains largely unexplored. In this paper, using a $d$-dimensional generalization to the fundamental lemma of Neyman and Pearson (d-GNP), we obtain the Bayes optimal solution for learn-to-defer systems under various constraints. Furthermore, we design a generalizable algorithm to estimate that solution and apply this algorithm to the COMPAS and ACSIncome datasets. Our algorithm shows improvements in terms of constraint violation over a set of baselines.

Sample Efficient Learning of Predictors that Complement Humans

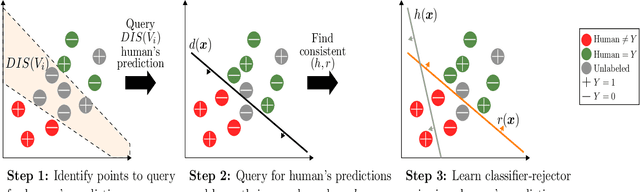
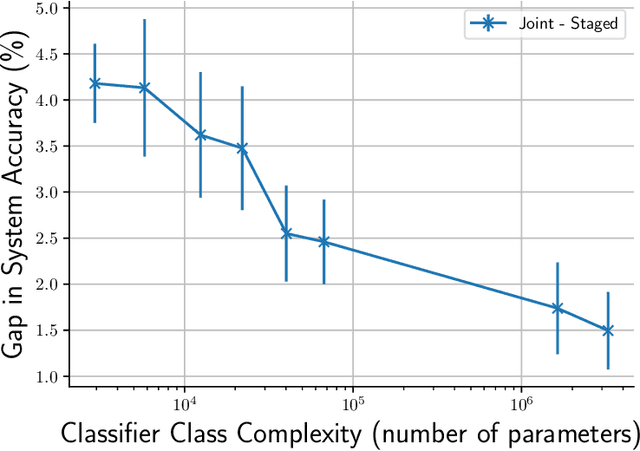
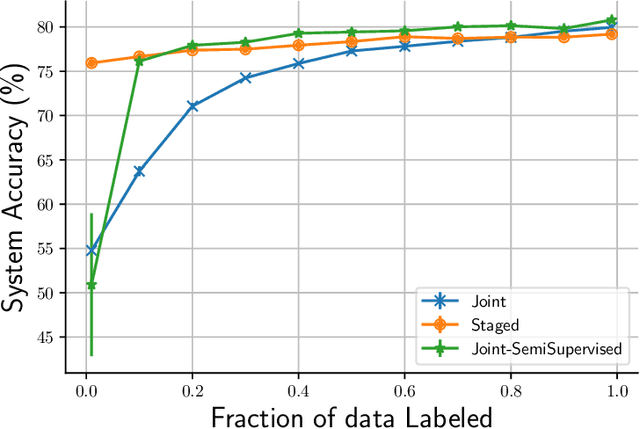
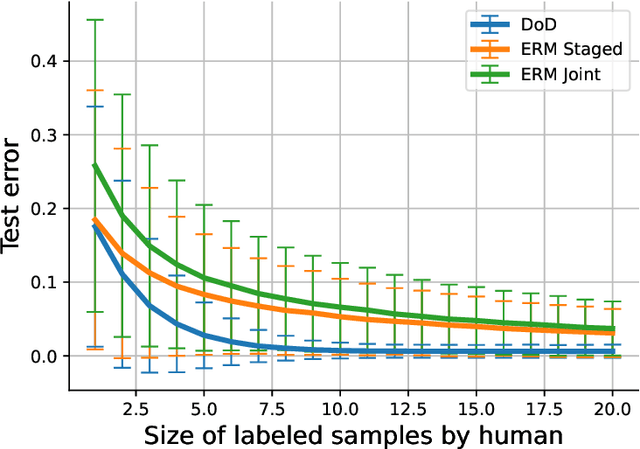
One of the goals of learning algorithms is to complement and reduce the burden on human decision makers. The expert deferral setting wherein an algorithm can either predict on its own or defer the decision to a downstream expert helps accomplish this goal. A fundamental aspect of this setting is the need to learn complementary predictors that improve on the human's weaknesses rather than learning predictors optimized for average error. In this work, we provide the first theoretical analysis of the benefit of learning complementary predictors in expert deferral. To enable efficiently learning such predictors, we consider a family of consistent surrogate loss functions for expert deferral and analyze their theoretical properties. Finally, we design active learning schemes that require minimal amount of data of human expert predictions in order to learn accurate deferral systems.

Polynomial magic! Hermite polynomials for private data generation

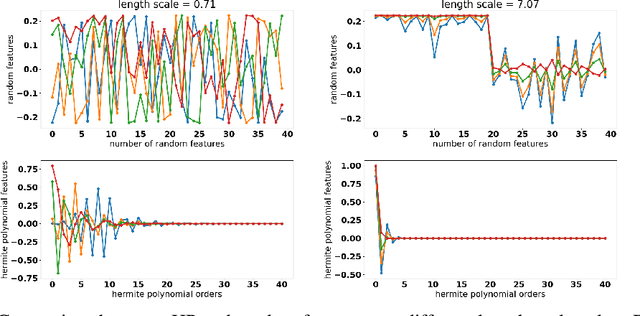
Kernel mean embedding is a useful tool to compare probability measures. Despite its usefulness, kernel mean embedding considers infinite-dimensional features, which are challenging to handle in the context of differentially private data generation. A recent work proposes to approximate the kernel mean embedding of data distribution using finite-dimensional random features, where the sensitivity of the features becomes analytically tractable. More importantly, this approach significantly reduces the privacy cost, compared to other known privatization methods (e.g., DP-SGD), as the approximate kernel mean embedding of the data distribution is privatized only once and can then be repeatedly used during training of a generator without incurring any further privacy cost. However, the required number of random features is excessively high, often ten thousand to a hundred thousand, which worsens the sensitivity of the approximate kernel mean embedding. To improve the sensitivity, we propose to replace random features with Hermite polynomial features. Unlike the random features, the Hermite polynomial features are ordered, where the features at the low orders contain more information on the distribution than those at the high orders. Hence, a relatively low order of Hermite polynomial features can more accurately approximate the mean embedding of the data distribution compared to a significantly higher number of random features. As a result, using the Hermite polynomial features, we significantly improve the privacy-accuracy trade-off, reflected in the high quality and diversity of the generated data, when tested on several heterogeneous tabular datasets, as well as several image benchmark datasets.